The History of ‘Histories’
Note that this piece was followed by an Addendum (26-Oct-2017) and both articles were built upon in Full Member Video Update #07 (3-Nov-2017).
The History of ‘Histories’
PROLOGUE
Before reading this article, you might benefit from revisiting earlier pieces regarding what I call the History Hoax and also Primary Source Research Methodology.
Article #19 | The History Hoax – A Primer (5-Jul-2017)
tl;dr Humans love stories, and the stories of ‘history’ are just stories. Even true stories are still just stories, and the retelling of stories requires no intelligence or genuine thought, but merely repetition. We have grown up in an age in which so many stories have been repeated so many times that few of us will ever stop to wonder, let alone investigate, where these stories actually come from.
Article #20 | The History of History (6-Jul-2017)
tl;dr The academic discipline known as ‘history’ is less than 200 years old. History ‘education’ dates to the 1800s, and yet ‘experts’ within that field can supposedly tell us what was happening hundreds and even thousands of years ago. And people believe them. That is, the ‘experts’ claim to have knowledge of events which are literally prehistorical.
Article #29 | Primary Source Research Methodology (17-Oct-2017)
tl;dr Primary sources are those which come directly from the time / event / person in question. Secondary sources are those which do not come directly from the time /event / person in question. It seems logical to sooner rely on a man’s own words/writings to piece together his life than to rely on stories told decades or centuries (or millennia) later. This is why I personally prioritise primary sources well above secondary sources in my research.
If you have not already done so, you are also strongly encouraged to familiarise yourself with the Exordium page and in particular the Welcome Video. If you haven’t revisited that page/video for some time it may be worth refreshing your memory.
NOTE: The images used in this article are likely to be scaled down if you read them on a handheld device. You can click on any image to see it in full size.
Herodotus is considered the ‘father of history’. My question is: did he even exist?
This article will use the example of ‘Herodotus’ and his classic work Histories to demonstrate just how little of what we are shown as ‘history’ is based on primary sources.
Contents
1 – Introduction to Herodotus (popular sources)
2 – Official stories and modern mythos
3 – Tertiary sources vs primary sources
4 – Wikipedia’s page on Herodotus
5 – Wikipedia’s page on Herodotus – references
6 – Godley’s translation of Herodotus
7 – Stein’s translation of Herodotus
8 – The process of primary source research
9 – Wikipedia’s page on Herodotus’ work Histories
10 – Wikipedia’s page on the Oxyrhynchus Papyri
11 – Oxford confirms the story of Oxyrhynchus
12 – The bust of Herodotus
13 – Key concepts and ideas revised
14 – There is no case – there never was!
15 – I know it sounds crazy, but…
16 – I could be wrong
Sources
Credits
1 – Introduction to Herodotus (popular sources)
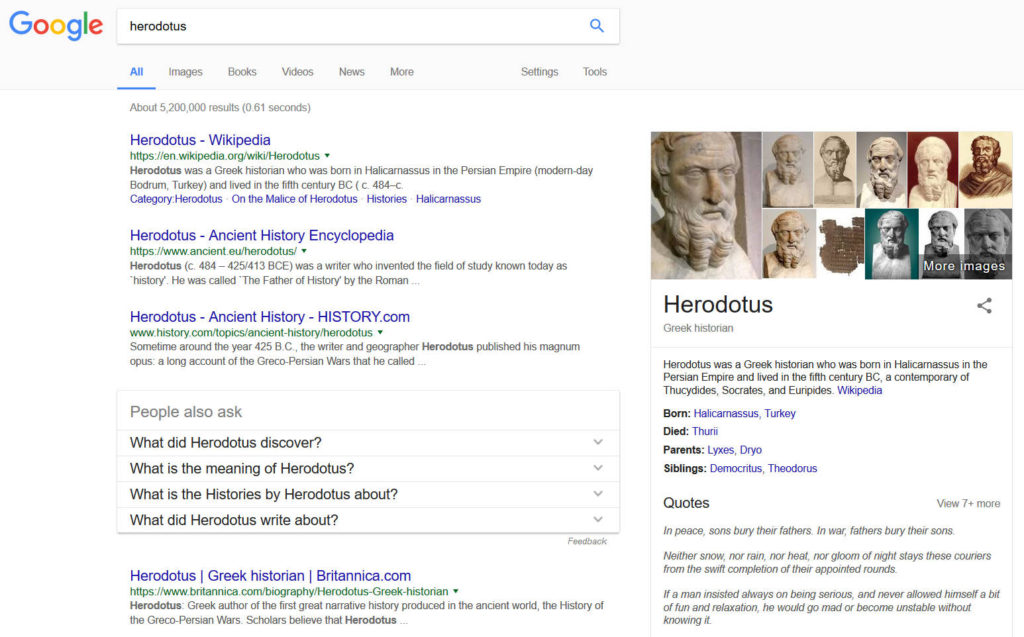
Herodotus is a key figure in the field of ‘history’. If one were to google his name, the top four search results would likely be pages from Wikipedia, Ancients.eu, History.com, and Brittanica.com.
Let’s take a look at what each has to say about ‘Herodotus’.
Wikipedia
Herodotus was a Greek historian who was born in Halicarnassus in the Persian Empire (modern-day Bodrum, Turkey) and lived in the fifth century BC (c. 484–c. 425 BC), a contemporary of Thucydides, Socrates, and Euripides. He is often referred to as “The Father of History”, a title first conferred by Cicero; he was the first historian known to have broken from Homeric tradition to treat historical subjects as a method of investigation—specifically, by collecting his materials systematically and critically, and then arranging them into a historiographic narrative.
–link
Ancients.eu
Herodotus (c. 484 – 425/413 BCE) was a writer who invented the field of study known today as `history’. He was called `The Father of History’ by the Roman writer and orator Cicero for his famous work The Histories but has also been called “The Father of Lies” by critics who claim these `histories’ are little more than tall tales. Criticism of Herodotus’ work seems to have originated among Athenians who took exception to his account of the Battle of Marathon (490 BCE) and, specifically, which families were due the most honor for the victory over the Persians. More serious criticism of his work has to do with the credibility of the accounts of his travels.
–link
History.com
Sometime around the year 425 B.C., the writer and geographer Herodotus published his magnum opus: a long account of the Greco-Persian Wars that he called The Histories. (The Greek word “historie” means “inquiry.”) Before Herodotus, no writer had ever made such a systematic, thorough study of the past or tried to explain the cause-and-effect of its events. After Herodotus, historical analysis became an indispensable part of intellectual and political life. Scholars have been following in Herodotus’ footsteps for 2,500 years.
–link
Brittanica.com
Herodotus (born 484 BCE?, Halicarnassus, Asia Minor [now Bodrum, Turkey]?—died c. 430–420), Greek author of the first great narrative history produced in the ancient world, the History of the Greco-Persian Wars.
–link
Putting this all together, then, the following would seem to be a fair summary of the official story overview of Herodotus.
-Alive roughly 400 BC
-the ‘father of history’
-the man who ‘invented the field of study known as history’
-the man whose ‘footsteps have been followed by scholars ever since’
-his work Histories is the ‘first great narrative’ of history
KEY: Herodotus is a central figure of ‘ancient history’ and is considered by popular sources to the ‘father of history’.
2 – Official stories and modern mythos
It is beyond the scope of this article to explore the concept of the ‘official story’ (that is, the mythos intended for and/or accepted by the masses), or how the modern layman will typically source his information from the top few results of a google search. It should suffice for now to point out that the four paragraphs provided above can be taken as an overview of the official story of Herodotus as it stands today. That is, as far as a regular person would be concerned, the information cited above would be considered to be a genuine, historical account of the life of Herodotus.
3 – Tertiary sources vs primary sources
Each of the four sources in question are what I would describe as tertiary sources. That is, compilations of secondary sources (and, in theory, primary sources) for the purpose of a broad overview of the topic at hand. Ideally, a tertiary source will provide a ‘bibliography’ and/or ‘references’ for inquiring minds to dig deeper into the matter for themselves.
In the case of historical figures it is obviously going to be worth going directly to the primary source i.e. the words of the historical figure himself. Since we cannot read ancient Greek, we will have to settle for translations. So long as these translations are themselves based upon the original, primary sources, and can cite the whereabouts of the original (so that those who wish to do so can check for themselves), then these translations are as good as primary sources for the purpose of our investigation.
KEY: Since we cannot read ancient Greek, we will accept as a ‘primary source’ a true translation of Herodotus’ words — so long as the original can itself can be identified for verification.
This ought to be straightforward. If I were to publish a translation of somebody else’s work, I would obviously explain at the outset which copy of their work I had used as my source. If I were translating a book, I would explain at the very beginning of my translation, as part of the preface (if not earlier), which original book I was translating from, where I had gotten the book, and where others can go to find the original for themselves. This is not just good scholarly practice; it is common sense.
4 – Wikipedia’s page on Herodotus
Now let’s take a look at the supporting information provided by the Herodotus page on wikipedia.
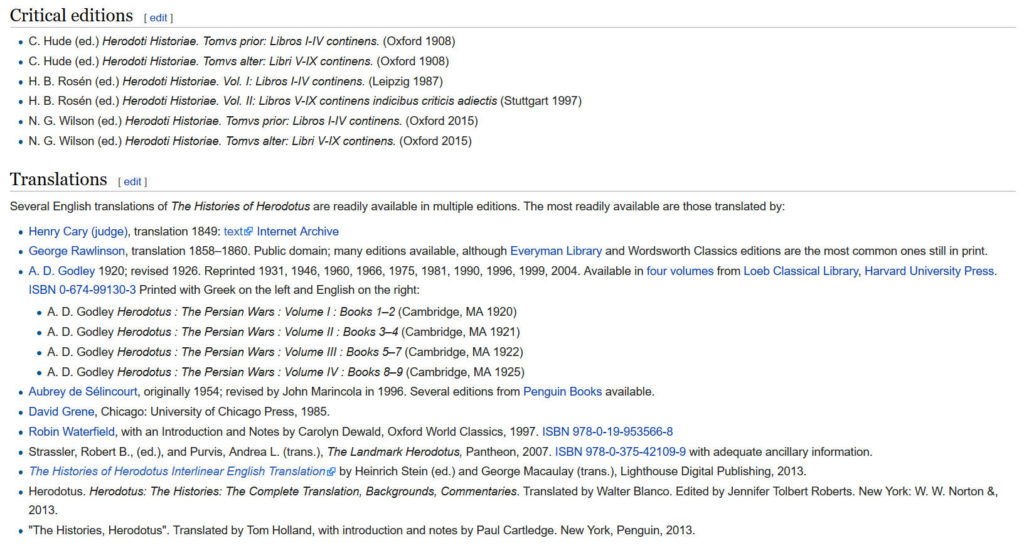
To the untrained eye, this certainly seems impressive. It looks so academic and formal: all of those dot points, ISBNs and italicised words. Fancy.
Now let’s take a closer look: the oldest English translation on that list is from 1849. The oldest critical edition is from 1908.
English is supposed to be at least several hundred years old. According to history, William Caxton was printing in English in the 1400s, and the King James Bible was printed in English in the 1600s. Does it strike you as peculiar that the oldest listed translation of the most important work of ‘history’, written by the ‘father of history’, entitled Histories, is dated to 1849?
Think about this for a moment. The people you are surrounded by every day get their ‘knowledge’ from the TV and, if they are curious to learn more, from websites like Wikipedia.
The wikipedia entry for Herodotus, the top result if one googles ‘Herodotus’, lists as the oldest critical edition or translation, a book from 1849.
KEY: The oldest translation of Herodotus’ Histories listed by his wikipedia page is from 1849.
5 – Wikipedia’s page on Herodotus – references
Now let’s take a look at the references from that same wikipedia page. These are the sources cited within the article itself. Every major claim made within the article is supposed to be referenced, and the references should effectively provide the curious reader with a clear indication as to where the purported information can be found and verified.
Most people do not bother to check the references of the wikipedia articles they read. It is my opinion that 99+% of visitors to the wikipedia page in question will never attempt to verify even a single reference. The fancy-looking footnotes will, however, bestow an air of credibility and academic rigour to the article. That is, the footnotes/references make the article look legitimate to the untrained eye.
But just how legitimate are these references?
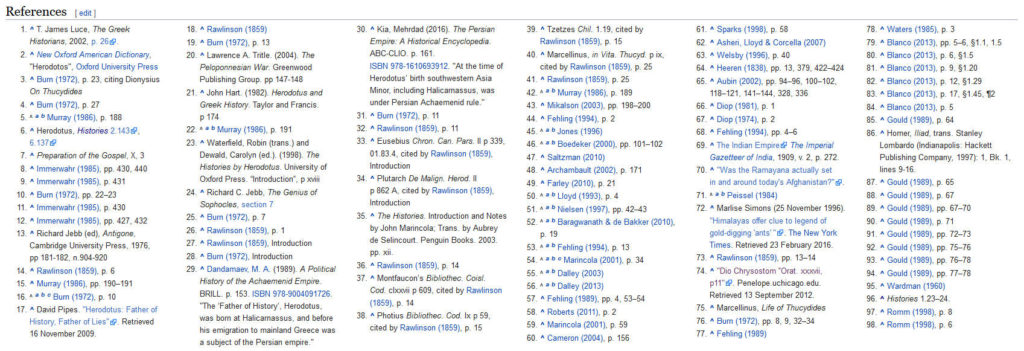
The first thing you might notice is that most of these sources are relatively recent, dated from the 1970s through to today.
In fact, of the 98 references cited throughout the article, more than three quarters are explicitly dated within the last fifty years.
The bulk of the remainder are references to Rawlinson (1859).
The second thing you might notice is that these references are, with just a few exceptions, all secondary/tertiary sources.
In fact, of the 98 references cited throughout the article, only two of them are to Herodotus’ Histories.
Put another way, in the entire wikipedia entry for Herodotus, only two of the 98 references go directly to the words of the man in question.
The tiny proportion of people who follow those two references to their source will find that they are from a 1920 translation by A. D. Godley.

KEY: Of the 98 references cited in this wikipedia article about Herodotus, only two are to Herodotus’ own work (i.e. primary sources), and both of those references are in fact to a 1920 translation of Herodotus’ Histories.
This alone should raise red flags in the mind of any objective, rational, thinking person. How can a multi-thousand word article about any figure of history – let alone the ‘father of history’ – contain only two direct references to words of the man in question? And why are those two references both to a source which is itself less than 100 years old?
6 – Godley’s translation of Herodotus
In any event, let’s take a look at that translation by Godley. Not only it is the only ‘primary source’ (direct) reference to Herodotus in the entire wikipedia article about him, but is is also one of the oldest sources listed in the Translations section.
Godley’s book is available in pdf from archive.org.
What we want to know is, what is the actual primary source on which Godley based his translation? Which work of Herodotus did Godley use to create his translation? Was it a manuscript stored in some exclusive library? Godley must have gotten his hands on a Herodotus original, surely…

…no. Godley’s translation is actually based on Stein’s translation. The image above is a screenshot of the pdf linked earlier, page xvii.
“The text which I have followed is that of Stein; in the few passages of any importance where I have thought fit to follow any other authority, the fact is noted.”
In other words, Godley’s translation is not of Herodotus’ words, but of Stein’s words, which are themselves supposedly a translation of Herodotus’ words.
You’ll note that Godley openly states that the ‘best’ sources are dated to the tenth and eleventh centuries.
KEY: Even on the most generous reading, the ‘best’ accounts of ‘Herodotus’ are from the tenth century i.e. 1400 years after his alleged existence.
7 – Stein’s translation of Herodotus
The more pressing concern is that Godley’s ‘translation’ is in fact based on somebody else’s translation. Let’s put that into a simple schematic:
Wikipedia -> ‘Herodotus’ -> Godley (1920) -> Stein (1883) -> Herodotus?
Remember that the entire wikipedia ‘Herodotus’ article contains 98 references but only two of them go to Herodotus, and as we can see here, they don’t really go to Herodotus: they go to Godley who in turn goes to Stein (who, we might be led to believe, at least sourced his translation from Herodotus).
Okay then, let’s see if Stein did indeed base his own work on the direct account of Herodotus.
After some digging I found a pdf copy of Stein’s work at the internet archive. It is dated to 1883 and printed entirely in German.
I don’t presently have sufficient time to type out the German from that pdf into google translate. If I did have that time, I would like to know where Stein claims to have found the original work of Herodotus – if indeed he claims to have based his work on Herodotus to begin with. I would not be the least bit surprised to find out that Stein either:
a) Offers no explanation of where he got his information, or
b) Admits that his own work is based on some other person’s ‘translation’
As it stands, we have spent some time tracing the sources given to us by wikipedia. Only two of the 98 references are to Herodotus, but neither of these are directly to Herodotus: they instead go to Godley’s 1920 translation. But Godley’s translation is not a translation of Herodotus, it is a translation of Stein. I can’t determine if Stein even claims to have based his translation on an original, because it is written entirely in German.
Again, look at what we are dealing with here, and bear in mind that ‘Herodotus’ is the ‘father of history’.
KEY: Wikipedia -> ‘Herodotus’ -> Godley (1920) -> Stein (1883) -> Herodotus?
8 – The process of primary source research
Tracing back to the primary sources regarding historical figures is incredibly time-consuming and laborious.
By now you may be getting some idea of how frustrating this type of research – that is, real research – can be, particularly when dealing with ‘history’.
Each step along the way, nobody has been upfront about their primary sources. None of the sources or authorities inspected so far have stated clearly, at the outset of their work, whether or not their information comes directly from Herodotus. If you put aside some time to try this for yourself, you will see the same pattern repeated over and over again.
Pick a character from ‘ancient history’.
Google searches will bring up tertiary sources such as wikipedia and Brittanica. These tertiary sources will cite and refer to other tertiary sources, and myriad secondary sources. They may occasionally refer to ‘primary‘ sources, but those ‘primary’ sources – when scrutinised – will in fact turn out to be secondary sources (generally written within the last 150 years). Those secondary sources will generally not be upfront about where they got their information; it will usually require copious reading through the preface/introduction/body of the text to find an explanation about the basis for their claims (if indeed any explanation is given at all).
It is like trying to make sense of a murder case in which every ‘witness’ bases his story – when asked – on hearsay from other ‘witnesses’. You want to know what happened at ‘time x’ and ‘place y’ and, although there are plenty of people claiming to know the truth, every single ‘witness’ depends on the testimony of somebody else. Did anybody actually see what happened? Can we talk to that guy? Or at least read what he wrote down? Did he write anything down at all? Has anybody seen it? Sure, but you’re going to have to talk to this other guy first, or read the translation of it from a book which doesn’t explain when or where the translator saw the original!
Note that none of the Ancient.eu article, History.com article, or Brittanica.com article provides a reference list or bibliography. The wikipedia page we have just dissected is the most ‘academic’ or ‘rigorous’ of the lot. Think about that for a moment.
KEY: Tracing back to the primary sources regarding historical figures is incredibly time-consuming and laborious.
It is worth pondering just why this might be the case…
9 – Wikipedia’s page on Herodotus’ work Histories
Now let’s take a look at wikipedia’s entry for Histories, the great (and only known) work by Herodotus. Perhaps this wikipedia entry can tell us where to find the original Herodotus (or, at least, where we can find the oldest copy of his work still in existence).
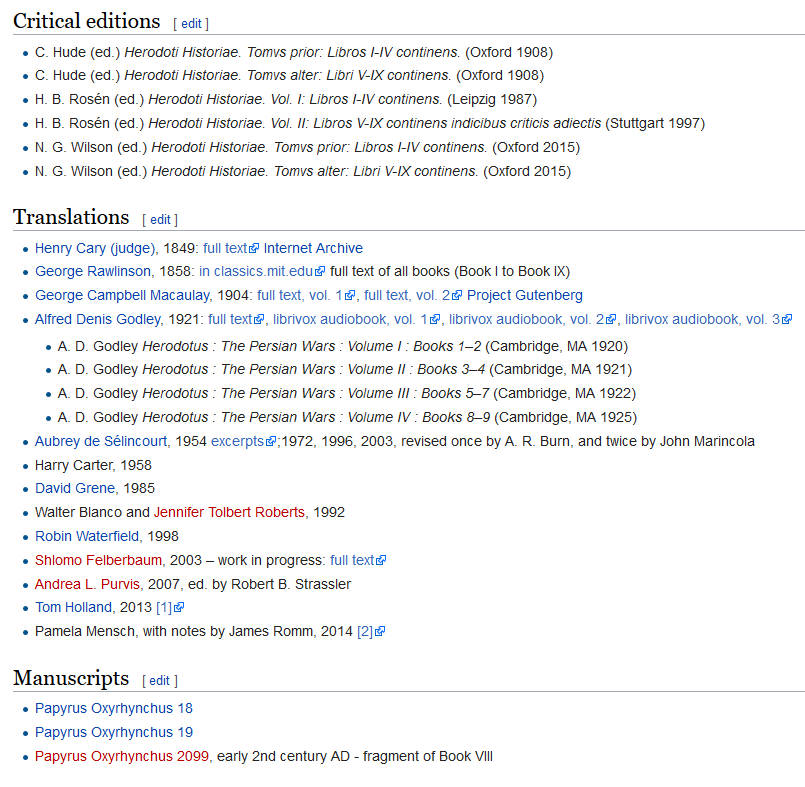
You’ll note that the Critical Editions and Translations lists are almost identical to those offered on the Herodotus page seen earlier.
Of interest to us is that this page does list Manuscripts i.e. the actual primary sources. Huzzah! We are getting somewhere!
The manuscripts of Herodotus’ Histories come from the ‘Papyrus Oxyrhynchus’, and we are even given specific numbers: 18, 19 and 2099.
Now that sounds serious.
Finally, JLB’s own research has debunked his theory that ancient history is all make-believe.
You may be smirking: ‘sucked in, smarty pants!’
There’s just one little problem…
ARE YOU READY FOR THIS? THERE’S NO TURNING BACK NOW…
No refunds. No apologies. You had your chance to turn back. I warned you. Oh how I warned you.
After seeing this, there will be no returning to Normieville as though nothing happened.
No listening to the truth clowns and truth charlatans who pretend to know what is actually going on.
Keep reading and you will be with me on the ‘other side’.
It is nice here, but there are not many of us. It can be lonely sometimes.
10 – Wikipedia’s page on the Oxyrhynchus Papyri
You might be wise enough to ask at once: What are the ‘Oxyrhynchus Papyri’?
What I am about to share with you, I first discovered for myself in early 2016.
But don’t let me spoil it for you. Go and take a look at the wikipedia page for yourself.
Go on, check it out. Come back here when you have had a look at it.
PLAY ALONG AT HOME
Seriously, go and take a look for yourself before reading the rest of this article. It will be more fun this way.
What did you notice?
When did Grenfell and Hunt ‘discover’ these papyri?
The late 1800s and early 1900s.
But that is less than 150 years ago!
Now how is this possible?
Surely Grenfell and Hunt’s papyri are not the alleged ‘primary sources’ which underpin the story of the ‘father of history’.
There is no way that 120-year-old papyri could be central to the official narrative of ‘ancient history’…
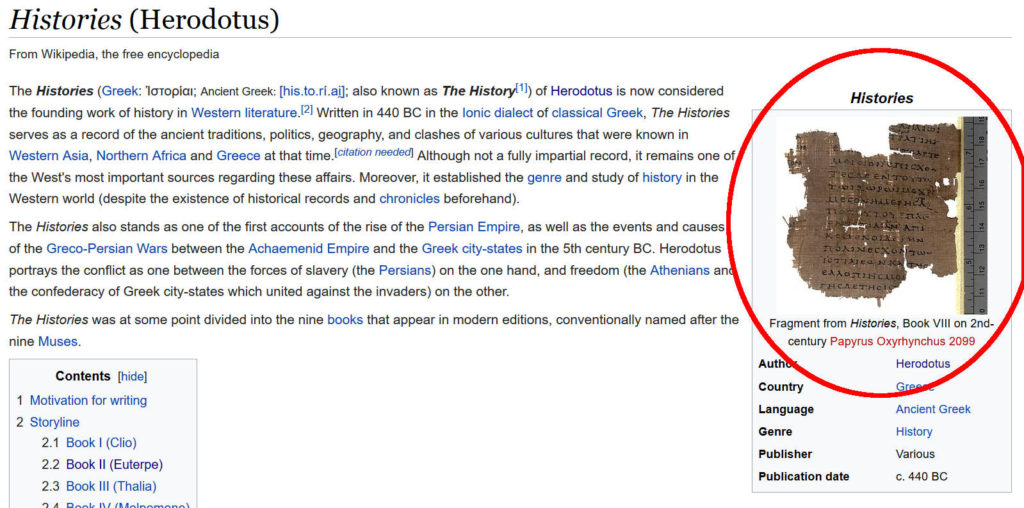
It could be a complete coincidence that the ‘papyrus’ used as the header image for the Histories page on wikipedia is itself from the Papyrus Oxyrhynchus.
Perhaps they have the real deal, an actual ancient text, sitting elsewhere, and they just used this as the header image for… ‘illustrative purposes’.
Perhaps.
Think about how the average lemming would perceive this wikipedia page. Think about how legitimate the image appears to the untrained eye. Think about how academic the words ‘Papyrus Oxyrhynchus 2099’ must seem to a man who does not know any better. Think about how much trust your fellow ‘human’ has in establishment, authority figures such as ‘historians’ — or, in the case of Grenfell and Hunt, ‘Egyptologists’.
Does the Lie System really need to reveal anything more than some papyri ‘discovered’ 120 years ago in order to convince the masses? Is anybody other than myself ever going to doubt these stories? Or spend the time required tracing back through the tertiary sources to the secondary sources, and then read through the secondary sources trying to find the primary sources?
My answer is no: TPWRTS do not need anything more than this. 2,400 years of ‘History’ can be created out of thin air — or ‘discovered’ the sands of ‘Oxyrhynchus’ in northern Africa by a couple of friends from Oxford.
Those who were children when Grenfell and Hunt made their amazing discoveries are all dead now.
In the time which has passed since then, ‘History’ has become reality.
And so much of our ‘reality’ today is premised on the notion that human civilisation is thousands of years old.
The average person alive today is convinced, on a fundamental psychological level, that civilisation is thousands of years old.
It is part of his worldview, the framework by which he understands and interacts with the world around him.
Like the fish who does not even notice he is swimming in water.
Ask the average normie if it is even possible that ‘ancient Egypt’ as we know it is make-believe. Go on, I dare you.
KEY: The ‘papyri’ which serve as the primary source evidence for Herodotus were ‘discovered’ around 1900 in Northern Egypt by two dudes from Oxford.
11 – Oxford confirms the story of Oxyrhynchus
Want to know more about this magical find of ancient documents? Look no further than Oxford’s own ‘Virtual Exhibition‘:
Almost nothing of [ancient Oxyrhynchus] remains. The stone was carted away for use elsewhere or burnt to produce lime to spread on the fields. A modern village now occupies part of the site. What Grenfell and Hunt found was the rubbish of Oxyrhynchus, which had been carried out and piled into a heap until it became more convenient to start another heap elsewhere, and so on. In the huge rubbish heaps were papyri, sometimes by the basketful, many rotted and fragile, but in such numbers that it took six seasons of excavation to bring them away. 65 volumes with transcripts, translations, and commentaries on the texts have been published so far. Vol. 66 is in preparation.
Yes, the papyri which Grenfell and Hunt ‘discovered’, thousands of years old, was actually the rubbish of ancient Oxyrhynchus. Still in good enough condition to read and translate, which the fine folk at Oxford have been doing, slowly but surely, ever since. What great fortune.
You can see a copy of the 1898 book released by Grenfell and Hunt about their discoveries here.
KEY: Oxford has an entire website section dedicated to Grenfell and Hunt, and their pioneering of ‘papyrology’.
12 – The bust of Herodotus
Are you ready for more? Let’s take another look at the header image for the wikipedia entry for Herodotus himself.
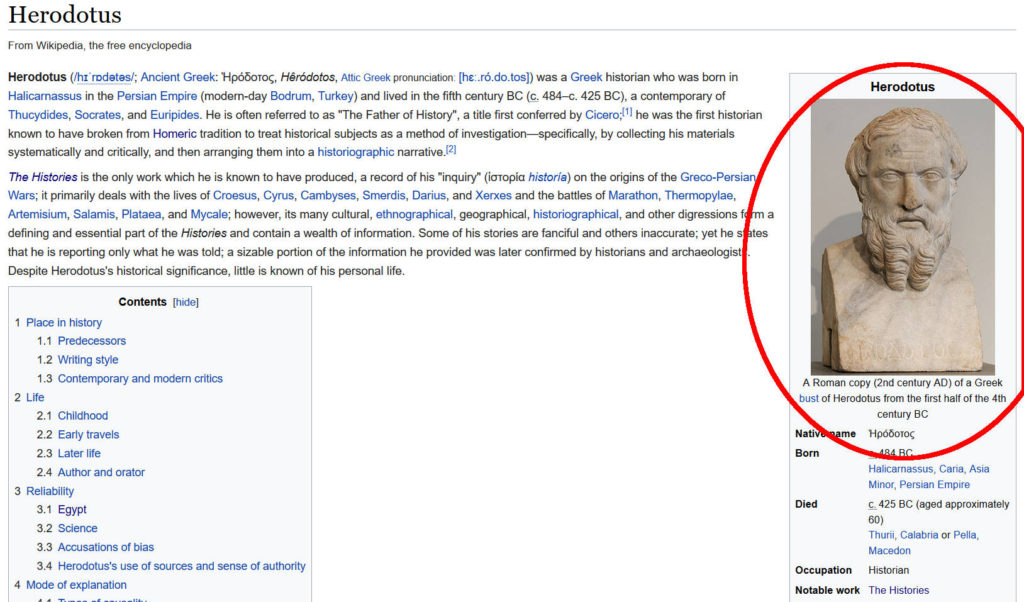
Wow, that bust sure looks legitimate. Okay, it is a ‘Roman copy’, but the copy is still from 200AD, which is certainly more than 150 years ago, JLB!
‘How do you explain that one?’, you might ask.
Why don’t you tell me? Here is the relevant webpage of the Metropolitan Museum of Art, where the piece is on display.
Take a look at that page and tell me what you notice. Come back here once you have had a gander.
HAVE SOME FUN
Go on, take a look at the page for yourself. It really is more fun this way. Trust me.
Did you check the ‘provenance’ section? If so, you might have noticed this:
“Shortly before 1891, found in Benha (ancient Athribis), Lower Egypt, by Émile Brugsch Bey; 1891, purchased by George F. Baker, acquired in 1891, gift of George F. Baker.”
Discovered in the late 1800s. Well I would like to say that I’m surprised.
But you know I’m not.
For a bit of extra fun, here is the wikipedia entry for Mr George F Baker, the man who purchased and donated the bust.
Want some more fun? Here is the wikipedia entry for Emile Brugsch, the man who supposedly ‘discovered’ the bust.
KEY: The bust of Herodotus, the main image on his wikipedia page, was also ‘discovered’ in the late 1800s.
13 – Key concepts and ideas revised
Herodotus is a central figure of ‘ancient history’ and is considered by popular sources to the ‘father of history’.
Since we cannot read ancient Greek, we will accept as a ‘primary source’ a true translation of Herodotus’ words — so long as the original can itself can be identified for verification.
The oldest translation of Herodotus’ Histories listed by his wikipedia page is from 1849.
Of the 98 references cited in the wikipedia entry on Herodotus, only two are to his own work (i.e. primary sources), and both of those references are in fact to a 1920 translation of Herodotus’ Histories.
Even on the most generous reading, according to Herodotus scholars, the ‘best’ accounts of ‘Herodotus’ are from the tenth century i.e. 1400 years after his alleged existence.
Wikipedia -> ‘Herodotus’ -> Godley (1920) -> Stein (1883) -> Herodotus?
Tracing back to the primary sources regarding historical figures is incredibly time-consuming and laborious.
The ‘papyri’ which serve as the primary source evidence for Herodotus were ‘discovered’ around 1900 in Northern Egypt by two dudes from Oxford.
Oxford has an entire website section dedicated to Grenfell and Hunt, and their pioneering of ‘papyrology’.
The bust of Herodotus, the main image on his wikipedia page, was also ‘discovered’ in the late 1800s.
Note: This article has used Herodotus (and his Histories) to demonstrate what I am talking about when I refer to the ‘History Hoax’.
This is just the tip of the iceberg.
14 – There is no case – there never was!
By now the regular visitors to this website will be aware that Dark City (1998) is among my favourite films.
You will find Eddie in the banner of the site (yes, he’s there somewhere) and I have made reference to this particular scene many times.
It even features in the Welcome video which I recommended you watch (or re-watch) in the prologue of this article.
15 – I know it ‘sounds crazy’, but…
My friends, I have been slowly but surely coming to terms with this for the best part of two years now.
‘Ancient history’ is all make believe. It never happened.
Or, at least, the ‘evidence’ on which these stories are based is incredibly recent and entirely unconvincing.
If you are willing to put in the time and effort to trace through the sources, as I have done, you can prove it for yourself.
It just takes time. Lots of time.
And it is a frustrating process. Dead-ends everywhere. As though the entire field of ‘history’ is designed to make it difficult to do what I have done here.
Tertiary sources which link to tertiary sources, secondary sources which rely on secondary sources.
Entire, elaborate stories about the lives of men who whose actual words are few and far between.
Time after time. Event after event. Figure after figure. All based on scant (and sometimes non-existent) ‘primary’ evidence.
Primary evidence which has usually been ‘discovered’ in the last 150 years.
And nobody else knows about this.
At least, not in our little corner of the internet.
I can only imagine that secret schools and elite organisations are well aware that history is a hoax.
Then again, I am also open to other possibilities. It may be that even those near the ‘top’ are oblivious, a’la the the Outer Party in George Orwell’s 1984.
It may even be that those at the very ‘top’ are oblivious, as was to be the case in The Village (2004).
I can go into more detail about this another time.
Either way, among those on our level, it is my honest suspicion that the only people who know what I am sharing with you now are myself, yourself, and whoever else is subscribed to this website and takes the time to read these articles.
We are talking a few dozen people, tops.
Millions (‘billions’ – lol) of people around the world, thousands of independent ‘researchers’ and ‘truth-tellers’ on the internet…
…and you could fit the number of people who know about all of this (at our level) into a decently-sized lounge room.
16 – I could be wrong
Please, prove me wrong.
It is possible that I have overlooked something, and it is also possible that I have completely lost my mind.
Find the evidence that I have failed to find. Track down the proof that Herodotus was a real guy who ‘existed’ before the 1800s.
Have fun!
Read the Addendum to this piece
Member questions answered, more evidence revealed to demonstrate the hoaxery involved.
UPDATES
3-Nov-2017: Herodotus, Histories, and related topics are central focus of Full Member Video Update #07 available here.
Useful Sources [to be updated]
Cary’s ‘translation’ (1876) – link.
Godley’s ‘translation’ (1920) – link.
Hereen’s book (1838) – link.
Stein’s ‘translation’ (1883) – link.
Credits
The production of this article, as with all new content on this website, was facilitated by the support of the following individuals. Without their financial contributions, none of this would be possible at this point in time. If there existed more people like the following, perhaps the ‘truth’ scene might not be so bereft of quality research and material.
(Full Members as at 24-Oct-2017)
Alistair Caine | alphaxomega | Big Dave | Chad628 | dbuser | Dante from NY | DJMoe1987 | G Malicious | Hando | Harry Ell | Jimmy Scoular | Jumpy64 | Nate M | local_chump | mas | Mezzie | Negentropic | PJG | Rebel | Shirt Ninja | Silvertree | Stansen | Sts1316 | TheProphet49 | TheyAreLaughingAtUs | Tikielimited | Tomfoolery | Wattzupsport
Production Notes
Originally published 24-Oct-2017.
Minor update (final proofread) 25-Oct-2017.
Addendum added 26-Oct-2017.
Released to Freeloader members 21-Aug-2018.
Very minor edits 10-Dec-2023 (vimeo video lost, replaced with youtube).
Original article written entirely on 24-Oct-2017, mostly at cafe, partly at home.
Made available publicly per JLBA #57 8-Dec-2020.
Slight update to the Addendum link at bottom of article 12-Mar-2021.



Very interesting article JLB. You are blowing my mind! I have some questions that I hope to get the chance to ask you on the next Skype call.
Thanks.
Feel free to ask your questions here. In many ways I can offer better responses via written format than in an off-the-cuff call.
OK JLB but I risk sounding stupid asking this question because the answer is probably obvious if I was paying close attention to what you wrote.
So here goes…..are you saying that the original primary source document for Histories is the Papyrus Oxyrhynchus discovered in 1900 but the Primary source documents cited in Wikipedia are translations of the Papyrus Oxyrhynchus supposedly done before the Papyrus Oxyrhynchus was discovered (Henry Cary (judge) 1849, George Rawlinson 1858, and H Stein 1883)? How could these individuals translate a document before it was actually discovered? If they were not translating the Papyrus Oxyrhunchus what were they translating?
I have now moved this reply to its own article/post, available here.
JLB thank you so much for making me feel comfortable in asking questions. I confess sometimes I have felt intimidated by your intellect as if you are playing 4 dimensional chess and I am still stuck on the 2 dimensional chess board. What you have presented here is an amazing case study for your history hoax theory. I have never seen anything like this kind of inquiry and research you have shown. It is truly amazing. I am in awe of the amount of work you have put into this article and the level of detail you have documented. If you are right about your history hoax theory it changes everything we have ever known or thought we have known.
Your response to my question is so amazing that is deserves to be in the body of the article. You might consider making this article a living case study and challenge anyone to debunk it. Allow it to grow and evolve as you come across more information as a result of your research. This article deserves to be seen by the mainstream public because this is paradigm shifting stuff. I wish there was a place on the internet where something like this could be crowd sourced to try to be debunked by historians and language experts. Surely anyone with a history degree would be fascinated by this kind of case study and would not be able to resist to try to debunk it.
Thank you so much for the time you put into this. What greater hoax could there possibly be than this?
Thanks again for the kind words.
You ought to remember that I have been doing this for several years now. When others are watching TV, I’m doing this. When others are out drinking, I am doing this. When others are with family, I am doing this. When others are watching YouTube videos, I am doing this. Three years is not long but I have seen and read and done an awful lot in that time, comparatively speaking.
Go back and listen to the early ARP episodes and you will see I was practically a normie.
My point is that all of us on this site are slowly but surely coming to terms with just how utterly deceived we have been by the ‘system’. Some of us may be at different stages along the journey but I don’t think anybody here, and certainly not myself, will judge anybody for asking questions or ‘look down’ on others for trying to improve themselves.
That is what I hope we are all here for. And I still have a looooooooong way to go.
I have gone ahead and created a stand-alone post for the comments, now entitled The History of ‘Histories’ [Addendum]. It ended up at over 3,000 words on its own, so it was rather foolish of me to not post it as a standalone in the first place.
Re the masses
This article deserves to be seen by the mainstream public because this is paradigm shifting stuff.
Here I will have to politely disagree. How will this shift anybody’s paradigms?
What do you expect or imagine might happen if I were to release this material publicly?
Please indulge me, I am interested to know what you believe would happen if I were to promote the History Hoax line of research to the masses.
Re the ‘experts’
You might consider making this article a living case study and challenge anyone to debunk it… I wish there was a place on the internet where something like this could be crowd sourced to try to be debunked by historians and language experts.
What exactly is there to ‘debunk’? All I have done is laid out a long list of ‘translations’ which either openly admit they are not based on the original, or simply fail to state what they are based on.
Many ‘translations’ by different authors across centuries, and all of them suffer from this same fatal flaw.
From this fact, which I think I have demonstrated beyond doubt, I have formed a logical inference: there is no primary source. There is no original Herodotus.
Save, of course, for the amazing, David Elliott-like ‘discovery’ in Oxyrhynchus circa 1900 by two dudes from Oxford digging around a 2000-year-old old rubbish-dump.
What I am trying to say is that there is nothing to ‘debunk’ here. Not insofar as I understand the term ‘debunk’.
At best, somebody may be able to produce an alleged/claimed original of Herodotus. Then we may be able to scrutinise it, and the investigation continues.
An expert merely repeating the nonsense I have already addressed is not a ‘debunking’.
An expert restating the claims made in the books I have already read, and cited, is not a ‘debunking’.
Re the importance of doing our own thinking
The whole purpose of spending hours upon hours tracing the sources, and linking to them as I have done, is to avoid any potentially ‘debunkable’ mistakes.
My article is based on primary source research methodology, and has employed a simple evidence -> analysis -> logic framework of exposition.
Rather than worry about what ‘experts’ will say when presented with my inference, why not investigate this for yourself?
If what I am saying is TRUE, then why would you care what an ‘expert’ in bullshit has to say?
If what I am saying is FALSE, then you ought to be able to determine this for yourself.
Therefore it makes far more sense for you to attempt to scrutinise my claims for yourself BEFORE asking an ‘expert’ for his opinion.
By providing all of the links to the sources in question, and explaining the logic used to arrive at my conclusion, I am inviting you (and all other readers) to do just that: scrutinise my claims for yourself.
Are my links legitimate? Is my reasoning sound? Have I overlooked a relevant piece of evidence? These are questions you can answer for yourself without any need whatsoever to consult an ‘expert’.
I have spent many hours explaining my research methodology, and providing the sources which underpin my conclusion with regards to Herodotus.
If anything I have said is either factually incorrect or logically fallacious, then you (and any other reasonable person) ought to be able to work it out for yourself, without the need to have an authority figure do it for you.
That is basically the central message I have been trying to share via my work for several years now.
A thinking man does not need establishment-credentialed ‘experts’ to tell him what to believe!
Why would you spend a moment concerning yourself with their opinions, if you have not yet performed a thorough investigation into the matter for yourself?
Brilliant detective work, JLB, with fascinating and revolutionary discoveries. Bravissimo! ASAP I will examine the wiki page on Erodotus in Italian. Maybe I’ll find something there too.
Anyway, what about historical buildings, monuments, like the Colosseum, the pyramids, or even medieval towns, which are so numerous in Italy and in other parts of the “old world”, for example? What do you make of them? They do prove that more or less ancient civilizations existed, of course. I don’t think you’re questioning this obvious fact, but can you suggest or infer that they’re less old than they tell us, for example, or what?
Aren’t they the best primary sources at our disposal, after all? And what do you think they can tell us?
Thank you.
Anyway, what about historical buildings, monuments, like the Colosseum, the pyramids, or even medieval towns, which are so numerous in Italy and in other parts of the “old world”, for example?
I strongly encourage you to investigate these for yourself, employing a simple ‘primary source’-oriented research methodology as I have attempted to demonstrate with this piece.
It is my suspicion that the full force of these revelations can only be felt when an individual goes through the process for himself.
In some ways it is a little bit like walking through a maze. Walls on either side, and dead-end after dead-end in front.
Perhaps one must hit these dead-ends for himself, in his own time, see the walls with his own eyes, before he can truly appreciate his whereabouts in ‘time’.
My own experiences with this began quite some time ago now. At least eighteen months ago (I specifically recall a weekend dedicated to researching ‘ancient Egypt’) but probably sooner than that.
Therefore I am doing my best to convey this theory, this revelation, in such a way as might be existentially amenable to relative newcomers to the notion.
Even as recently as a week ago it seemed to me that one or more members of this site thought my ‘History Hoax’ theory was either a philosophical position (i.e. that I believed ancient history was ‘real’ but wanted others to check for themselves), a marketing ploy, an arrogant exaggeration, or some other kind of less-than-serious suggestion.
Those who calmly, and without distraction, read the 8,000+ words of the The History of Histories (plus Addendum) and spend at least some time checking the sources will soon see that this is no joke.
I’m treading a fine line here. I saw what the revelation of the heliocentrism hoax did to people, I know and remember what it did to me.
This stuff can be VERY disorienting, not simply in a psychological sense but an existential sense.
I’m still coming to terms with it, and I have had a lot of time to process it all. Certainly a lot more time than people who are only just opening their minds to this notion.
My point here is that I am trying to encourage you, and others who read my work, to engage in the process of ‘primary source research’ for yourself.
My reasons for doing so include this: at least by walking the maze for yourself, you may be able internalise the revelations in accordance with the present want or desire of your psyche.
A psyche which, no matter how smart or learned or wise we believe ourselves to be, has a power and force and nature of its own.
This process, I suspect, may be less likely to lead to negative internal consequences than merely having somebody else (i.e. me) dump it all on you at once.
I have researched the ‘Colosseum’. I have researched the ‘pyramids’. I have researched ‘ancient Egypt’ and ‘ancient China’ and on and on and on and on.
Sitting and waiting on my hard drive are several detailed documents, not unlike this article, on other topics of ‘ancient history’.
My research and conclusions will be shared later.
For now, I have shared and detailed my method. I have provided an example of the method being put into practise.
Herodotus, the ‘father of history’, is a perfect starting point for this line of inquiry.
It must be clear now that I am not joking or exaggerating.
Those who TRULY care about this, those who UNDERSTAND the significance of what is being revealed, will do the research for themselves now.
Those who cannot or will not put in the time required, have nothing to gain from reading more of my conclusions.
I hope this reply is received in the good spirit and intention with which it is intended.
“I have researched the ‘Colosseum’. I have researched the ‘pyramids’. I have researched ‘ancient Egypt’ and ‘ancient China’ and on and on and on and on.
Sitting and waiting on my hard drive are several detailed documents, not unlike this article, on other topics of ‘ancient history’”.
Mmm… So you are withholding evidence from the court, eh? That’s not good… 😉
Seriously, I get your point, and ASAP I’ll apply your method of research on my beloved Colosseum, so hopefully we’ll be able to compare notes.
And your evidence would better be good on that particular symbolic monument, or you’ll have to face the wrath of ancient Rome manifesting through one of her descendants. 😀
Hey JLB,
thank you for this very intriguing piece of work.
The Oxyrhynchus Papyri story is so odd. Aside of the fraction pertaining to Herodotus those papyri contain the works of major historical figures such as Aristotle, Sophocles and Euclid and major parts of the bible. So many buzzwords it almost hurts my head.
That’s at least a vertebra in the backbone of the history hoax. Note that the majority of fragments are yet to be deciphered and translated. That’s another variable which allows for arbitrary manipulation of the historical plot at any point in time. Need to fill gaps in the narrative or to add details? No problem: ‘Recent analyses of ancient writings by the papyrology department at Suckmydick University shine light on previously only vaguely understood periods of Greek history.’ Create a story, let a few years pass and it will have silently crawled into official history.
I always wondered how far up the hiararchy those originating the major part of our modern mythology are. One might suspect that those in the know only contribute to the truly original content. I would argue that there is no need to fill whole libraries with your fiction. Just create the major parts and the moronic masses will thankfully fill the gaps for you. Offer a few evenly distributed pivots and the retards will gladly spin the whole web around them. You just stand and marvel at their naivety and imagination once their backbones have been substituted by a firm believe in authority.
Nobody does proper research and people love their stories. The more lively, loud and colourful the better, the more details the better. Create a few props, ‘discover’ them, associate a name and a date with them and the rest will take care of itself it seems. The whole thing will soon have grown to such a complexity that cannot be easily overseen anymore. Whereever necessary add details.
To name an example: Thousands of pages have been written about Osama Bin Laden’s assassination while the amount of original information (‘primary resource’ is hardly an apt label for some trivial videos of bearded men) about this character is almost miniscule. Any time spent researching OBL’s magnum opus, even superficially, will make a monkey raise its eyebrows. Yet there they are, in libraries and train station book shops all around the world, available in every language, the million words about a fictional character. Is that the hidden hand at work or are people really that willfully ignorant? I currently tend to believe the latter.
This is a recurrent theme in my personal, very confusing search for truth. The generating set of information from which copious, unimaginably large volumes of material are subsequently drawn often times is very small. Yet, the material is so vast and unimaginably complex, intertwined, referencing itself and other fields that you can’t help but to feel lost. Still, there’s always a not-so-thoroughly hidden red thread that leads you thorugh the ebony castle to a giant pile of horse shit with a smileyface sign in front of it.
Funny enough, just yesterday I went to my university’s library and had a look into some books. Even after having been around that stuff for years it never fails to make me feel utterly stupid. You feel so tiny from inside the golden palace, the maze is infinitely large and you will get lost in the details if you do not know what to look out for. You accept your inferiority, bow down to the authority and their new set of axioms and begin a lifetime of futility, studying concepts and ideas that might have absolutely no relationship to reality. Be very gud, earn dollars, write books. Is getting lost in the details your whole fucking life that easy to pull off?
That’s at least an explanation of what I see when strolling along the floors of the physics department. Serious posters of the state of the universe after [arbitrary number here] Planck-Seconds, intrically designed, computed from carefully crafted simulations with awe-inspiring precision and accuracy. Right now I wonder if maybe we’re the fools after all. Can it really all be bullshit? Oh boy.. we’re in for so much fun.
Concerning the German translation of Histories by Heinrich Stein: He put’s Herodotos into context with other ancient figures of his period and directly references their works (such as Gellius and Eusebios on page one), makes remarks about the use of the greek languange by Herodotos and then jumps into the text. Nothing hinting to his sources that I could find.
Cheers.
Excellent comment. Your first on this site — you have set the bar high for yourself!
Nice avatar by the way. Made me laugh when I first saw it. Perfect.
The Oxyrhynchus Papyri story is so odd. Aside of the fraction pertaining to Herodotus those papyri contain the works of major historical figures such as Aristotle, Sophocles and Euclid and major parts of the bible. So many buzzwords it almost hurts my head.
All the big names are there! It is like there was a party going on and everybody who was anybody got an invite.
The party must have been a fizzer because the invite list ended up in the rubbish dump, along with all of their finest works 🙁
That’s at least a vertebra in the backbone of the history hoax. Note that the majority of fragments are yet to be deciphered and translated. That’s another variable which allows for arbitrary manipulation of the historical plot at any point in time. Need to fill gaps in the narrative or to add details? No problem: ‘Recent analyses of ancient writings by the papyrology department at Suckmydick University shine light on previously only vaguely understood periods of Greek history.’ Create a story, let a few years pass and it will have silently crawled into official history.
I could not have said this better myself. Those who look into this further for themselves will note how often Oxford University pops up. From my own research it appears that Oxford is at the heart of the History Hoax. How appropriate that two of their boys should be the ‘discoverers’ of the Oxyrhynchus Papyri. As you rightly point out, they can now release fragments to ‘plug the gaps’ as necessary.
It is like ‘the never ending story’, except this story is going backwards through time! The past just gets more and more colourful.
Thanks to the fine folk from Oxford, we know more about what was happening 2,400 years ago than the people who were alive at the time!
I always wondered how far up the hiararchy those originating the major part of our modern mythology are. One might suspect that those in the know only contribute to the truly original content. I would argue that there is no need to fill whole libraries with your fiction. Just create the major parts and the moronic masses will thankfully fill the gaps for you. Offer a few evenly distributed pivots and the retards will gladly spin the whole web around them. You just stand and marvel at their naivety and imagination once their backbones have been substituted by a firm believe in authority.
After reading this section I was tempted to add your comment as a second addendum. This is brilliant stuff.
And 100% on point.
The moronic masses spinning their own web of lies around themselves. Give them a rock, or a fragment of papyri, and watch the ‘experts’ write whole books on the past they allegedly reveal.
Then watch cohort after cohort, generation after generation, build upon this shaky foundation with their own interpretations, updates, revised editions, and comprehensive catalogues.
Within a relatively short period of time, nobody even remembers or cares about the original rock or the original piece of papyri.
Every year, thousands of poor fools around the world are graduating with ‘history’ degrees having never laid their eyes on so much as a single original source for their fanciful beliefs.
Some of them will go into academia and help create further layers of the story, with journal articles and contributions to new textbooks for the next crop of biological automatons to consume.
Almost like a game of Chinese Whispers, but on a grand scale, involving players who are so oblivious to the game that they will shout you down for suggesting that there is no Purple Monkey Dishwasher.
https://www.youtube.com/watch?v=o_o7UfqkNuU
Nobody does proper research and people love their stories. The more lively, loud and colourful the better, the more details the better. Create a few props, ‘discover’ them, associate a name and a date with them and the rest will take care of itself it seems. The whole thing will soon have grown to such a complexity that cannot be easily overseen anymore. Whereever necessary add details.
100%.
Funny enough, just yesterday I went to my university’s library and had a look into some books. Even after having been around that stuff for years it never fails to make me feel utterly stupid. You feel so tiny from inside the golden palace, the maze is infinitely large and you will get lost in the details if you do not know what to look out for. You accept your inferiority, bow down to the authority and their new set of axioms and begin a lifetime of futility, studying concepts and ideas that might have absolutely no relationship to reality. Be very gud, earn dollars, write books. Is getting lost in the details your whole fucking life that easy to pull off?
The university libraries are daunting indeed. When I was an undergrad, the first university I attended was Monash in Clayton (Melbourne). It is relatively modern (built in the ’50s and ’60) and the primary humanities library is ‘only’ a few floors tall. In the image below, the brown section on the right is the part of the building where the books are kept. I think it might have been four stories tall, maybe five.
(Before anybody says anything, yes, I do now see the pyramid-like glass element atop the entrance. It goes without saying that I was symbol-illiterate back then.)
I still remember the first time I had to go and locate a book in there; my experience was very similar to what you have described.
‘So much information, so many smart people, too much to learn, too much to know.’
Realistically, the vast majority of the books in these kinds of libraries will never be read. Many will be borrowed simply for some skim-reading and quote-mining (to keep essay markers happy) but in essence these books act more as props than as tools for learning. When I say ‘props’ I mean objects to convey a message by appearance, and that message is as you suggest: authority.
While I am sharing images of my alma mater, here is another image I found while googling just now:
It always struck me how sterile these buildings were, and I was vaguely familiar with the architectural style responsible for the aesthetics.
Only upon reflection, times like now, do I see how horrible this kind of setting is for a young mind.
Marxist in style, marxist in substance.
Sometimes I wonder how I made it out of that place alive and intact.
I suppose in some ways, I didn’t. Another topic for another day…
Can it really all be bullshit? Oh boy.. we’re in for so much fun.
The History Hoax isn’t even in the top echelon of the Hoax Hierarchy.
I have stated this during the group Skype calls but it may bear repeating a few times more, to a slightly larger audience: one of my major motivations for ‘getting clean’ (no alcohol, no weed, no drugs other than caffeine, no processed foods; basically the purest my body has been, and certainly much purer than 99% of the population) is to assuage any doubt or concerns which I (‘I’ now or ‘I’ in the future) or other people may have about my ‘state of mind’ at this critical juncture — this turning point — in my life.
I am feeling at once more disconnected from my fellow ‘humans’, and yet more ‘in sync’ with my environment, than I can ever remember feeling. It is like I am here, I am really here and whatever this existence is, it is very real and very alive, but the other humans in this existence with me, they are (with rare exception) alive in a ‘biological’ sense only.
If I or anybody else wants to dismiss what I am saying with ad hominem critiques of my supposed mental state or ‘health’, let them do so in the knowledge that my body and mind is more pure right now than theirs is.
And I have the video footage to prove it.
This realm is trippy enough without drugs. That is not to diminish or disparage drug use carte blanche but, for a solid 12-week period at least, a clear (or relatively clear) body and mind is well in order.
In fact I will go so far as to suggest that it is when our bodies and minds are under duress that we may find ourselves more likely to identify with the moronic masses and their insane beliefs and mindsets, because they are all under physical and mental duress as a matter of routine. They poison their minds constantly, every day, oftentimes oblivious to what they are doing. And so, when we are placing an increased toxic load on ourselves, we may be putting ourselves into a state more alike that of the lemmings, with obvious results.
Put another way, I am suggesting that, contrary to the beliefs held by many normies and conspiratards alike, it may be that we can only ‘see’ clearly when we are clean (or at least cleanish), rather than when on mind-bending drugs.
We find ourselves in uncharted territory. Fun indeed!
Concerning the German translation of Histories by Heinrich Stein: He put’s Herodotos into context with other ancient figures of his period and directly references their works (such as Gellius and Eusebios on page one), makes remarks about the use of the greek languange by Herodotos and then jumps into the text. Nothing hinting to his sources that I could find.
Thank you very much for this. It is yet another example of what I am talking about. They will either dive right into the ‘translation’, or spend a few cursory pages speaking about the importance of Herodotus, and the difficulty of translation, without any explanation at all as to what it is that they are ‘translating’ i.e. where they are translating from.
Excellent debut comment on this website, Stansen, and welcome aboard!
“Please indulge me, I am interested to know what you believe would happen if I were to promote the History Hoax line of research to the masses.”
If you wrote a book about the history hoax and found a good publisher to publish it I believe you would become rich and famous. I promise you I would buy your book and I suspect many other people would too. I find what you have written absolutely fascinating and based on your comments it sounds like you already have enough research material for a book. You are a good writer JLB and I am sure you could write a history hoax book in an entertaining way. It would be a challenge because most people would find reading all the historical references in your historical case studies only to arrive at a place of smoke and mirrors painstaking but it is compelling to do so because your theory that ancient history is bullcrap is so monumentally mind blowing that many people could not resist doing it. After you did your book tour and settle into your million dollar plus home in Cleveland, Brisbane purchased from your best selling book sales you would enjoy seeing the fallout of your book such as the shrinking or disappearance of history departments in universities and plummeting history book sales and their reclassification to fiction. The dog in your front yard would no doubt be very well behaved and any young man happening to leave a flyer in your mail box would surely be met by a friendly greeting from said dog.
“What exactly is there to ‘debunk’? All I have done is laid out a long list of ‘translations’ which either openly admit they are not based on the original, or simply fail to state what they are based on.”
debunk |dēˈbəNGk|
verb [with object]
expose the falseness or hollowness of (a myth, idea, or belief): the magazine that debunks claims of the paranormal.
• reduce the inflated reputation of (someone), especially by ridicule: comedy takes delight in debunking heroes.
Your idea or belief that ancient history is not supported by any credible primary source evidence is what would attempted to be debunked.
In my opinion your analysis of the history of Herodotus is a convincing example supporting your idea or belief that ancient history is not supported by any credible primary source evidence. I seriously doubt anyone could debunk your theory. It is clear from your article the fact that the Papyrus Oxyrhynchus is an authentic primary source document supporting the history of Herodotus is just as believable that a man can determine the mass of the earth by hanging two balls in a shed.
impressive work. by a wide margin this is my favorite part of the jlb operation.
printed, read and took notes on this last week.
i’ve come to terms now that this is how i best consume content, digest and excrete commentary of any kind – on the printed page. problem is i no longer have unfettered access to printers where i can get entire pdfs / books /articles for free as in years past.
will comment and ask some speculative questions before end of week.
just want to re-read again, along with the addendum.
It is heart-warming to imagine that somebody out there is studying my work the same way I study the work of others.
Paper. Pencils. Pens. Notes. Reflections. Revisions.
I look forward to your thoughts on the matter at hand.
One other detail I love is that it took them 6 years to “cart away” all the papyrus documents they found in that dump. Which conveniently allows plenty of time for writing down what they claimed the ancients wrote!
By including details like that in the official story, they would almost seem to be BEGGING people to start asking questions.
It is all so obvious, now, isn’t it?
Great comment by Stansen. Indeed, the useful idiots strengthen these hoaxes mightily, making the jobs of the initial hoaxers infinitely easier.
I’d like to share a few thoughts on some of the psychological dynamics that cause useful idiots to bolster the lies unwittingly or semi-unwittingly.
1) Conformity. A deep-seated fear is that of being expelled from the tribe. Some of us truth-seekers and contrarians are less affected by this. But for most people, holding unusual or unpopular ideas is psychologically uncomfortable.
2) Strong belief in authority/experts
3) Desire to live under benevolent rulers. “They would never do that.” “They would never lie.” This one is pretty strong among normies. Even JLB and the rest of us subscribers understand that knowing what we know has some negative side effects. But normies feel panic at the notion that the world is not as it seems. Not only do they use flawed research and logic and default to “true until proven otherwise,” they feel acute discomfort when unapproved or scary theories are even mentioned.
4) A related emotion is the desire to think of one’s self as smart and well-informed. Realizing that one is a dupe can be psychologically stressful enough that many people prefer, at least unconsciously, to remain duped!
5) Related to that is sunk costs. The longer and more expensive one’s education was, and the more “successful” one was at regurgitating lies or playing a career role in the system, the harder it is to see the truth and reject the lies.
6) Related to that is having something to lose. If you’re a professor or a TV newsperson or a pundit or a politician, you expose yourself to ridicule for considering “conspiracies.” So most people avoid it.
7) Desire for status. People ape those above them in the social hierarchy. If the Oxford Dons say Egyptology is real, then by golly London social climbers are going to agree. If the rich and famous say that discrimination against transgendered people is an urgent social issue, then by golly people will start virtue signalling about it on Twitter.
Etc.
So there are a lot of dynamics which pressure people to:
a) believe the lies
b) reinforce the lies by repeating them
c) suppress any doubts
d) etc.
I have two relevant reading recommendations for this community of subscribers, which I’ll share in the next comment.
Excellent comment. There is not really much more for me to add to it. The seven reasons are all valid and concise. Well done.
Would you mind if I used this as the basis for a public article/thread? I can post it with or without credit/attribution, as per your preference.
When did you realise (or begin to understand) that people are/were so stupid?
For me, I still remember the first time I read Gustave le Bon’s The Crowd. So many pieces of the puzzle fell into place. Yes, these are social creatures, and this element of their nature dictates their actions infinitely more than does the abstract concepts we might call ‘logic’ or ‘truth’. Once we understand the nature of these creatures, their behaviour makes perfect sense. If instead we continue to live in ignorance to this nature, then we will continue to be amazed, befuddled, and even depressed, by the utter stupidity of those by whom we are surrounded.
This is just how they are. It is also, if we are being honest with ourselves, how we are — at least to an extent. To this day I would prefer to be liked than disliked, and this must naturally affect the way I conduct myself around other people, in the sense that ‘truth’ must still be moderated/tempered when dealing with people who clearly do not want or need truth. As social creatures, this element of the human condition affects us all.
Here are two short pieces I think this community might find interesting.
The first makes the point that people with less to lose within the system are more able to see or state truths about the system. And also that the most important key to seeing truth is just the open-mindedness to consider multiple possibilities.
Here’s the first one: all about 9/11:
http://www.ranprieur.com/essays/911FAQ.html
A few quotes from it:
“In America there is no abstract belief that correlates more perfectly with social status than acceptance or rejection of the official story about 9/11. So by rejecting it, with one stroke I can keep myself on the margins, where the action is.”
“Every theory about 9/11 is a conspiracy theory. The dominant theory says that it was a conspiracy of Islamic extremists acting independently. It’s not necessary to believe a different theory, only to accept that the dominant theory could be a giant lie, and it soon becomes obvious that the operation was planned and managed from the inside.”
“It’s not intelligence or sanity that enables people to see through big lies. It’s imagination and social position. Stepping into the fringe, on any issue, is a great responsibility. If they lied about that, what else did they lie about? Suddenly you’re no longer a passive consumer but a full-time investigator, questioning and evaluating and filtering everything yourself.”
etc. It’s a good, short read. It gave me confidence and helped me realize that the burden of proof actually isn’t on the skeptic, it’s on the original claimant.
And I’ll put the second reading recommendation in the next comment.
And my second reading recommendation makes the point that we are psychologically wired to seek status above all else and certainly above truth. Status gets us more resources and better mates. And pledging allegiance to lies often confers status.
Note: he gets a little political but that’s not the point. The point is that our beliefs are informed by our desire for status more than by our rationality.
https://spandrell.com/2015/10/the-social-module/
A few quotes:
“An average human brain has much more neurons being used to scan the social climate and see how “Status Points” are allotted, than neurons being used to analyze patterns in reality to ascertain the truth.”
“The little radio in our brains which tells us how to optimize our status has a hard time keeping up. What people do is extract some abstract schema of what is high status now, and what leftist agitators are shouting about. The best strategy is to adopt some vague keywords from the conventional wisdom, and proclaim one’s loyalty to that, while leaving the door open for plausible innovations by new leftists. So yes! Racism is evil. Feminism is great! Global warming is a serious problem! Transsexuals? Well, I don’t know. But we’re a free country, right? Oh, you mean Bruce Jenner is in drag in the New York Times? Transsexuals are awesome! Pedophiles? Well… people can’t choose their orientation… I think.
You can’t blame people for being logically inconsistent; because they can’t possibly know anything about all these issues. Few have any experience or knowledge about evolution and human races, or about the history of black people to make an informed judgment on HBD. Few have time to learn about sex differences, and stuff like the climate is as close to unknowable as there is. Opinions about anything but a very narrow area of expertise are always output of your Status Points module, not any judgment of fact. People don’t know the facts. And even when they know; I mean most people have enough experience with sex differences and black dysfunction to be quite confident that progressive ideas are false. But you can never be sure. At any rate, you’re always better off toeing the line, following the conventional wisdom, and keeping your dear Status Points.”
Thanks for the link, it was an interesting read.
The author's central contention appears to be along the lines of, 'humans are more interested in assessing the social status of those around them, and maximising their own, than they are in concepts such as truth', and that this is largely taking place 'sub consciously' or without deliberate thought on the part of the human. If I have read the author right, then I completely agree with the contention.
What I would add is that the same humans have a phenomenal propensity to engage in spur-of-the-moment, ad-hoc, post-facto rationalisation of their own logical inconsistencies. They didn't agree with the higher status person just because he/she was higher status, they did so because they agreed with what was being said. 'But didn't you have a different opinion yesterday?' 'No, that was different.'
In other words, humans are operating in a constant state of self-delusion. Is it any wonder that most remain utterly oblivious about things like media fakery, when they are also oblivious to their own logical inconsistencies? This is why I like to remind myself to focus on thinking about thinking, and have spent considerable time over the past year or two producing content based on this very idea: thinking about thinking.
To give an example of how even 'awake' people easily succumb to the affect of 'status', take a look at how John Adams' recent revelations were received by the resident Fakeologists. <a href="http://fakeologist.com/blog/2018/04/02/fac448-john-adams-says-its-real/" rel="nofollow">Link 1</a>, <a href="http://fakeologist.com/blog/2018/04/02/john-adams-says-this-event-is-real/" rel="nofollow">Link 2</a>.
People like Gaia were quick to defer to John Adams, and defend his account. Why? They 'trust' him. Have they met him? No. So what do they trust? His status: John Adams has considerable status as the host of well-known show in the scene (Hoax Busters Call), a regular collaborator with Jay Dyer, and a man who has (apparently) read a lot of books, and speaks with a measured, almost-fatherly voice.
It has been truly amusing to watch the primitive minds behave in an entirely predictable fashion. I feel for Ab, though. He must ask himself how his valiant efforts have led to his being surrounded by idiots.
Good comments, rico!
That could be a post, your 7 reasons
I agree.
Perhaps something along the lines of, ‘7 Reasons Normies Can’t See’.
Yes, of course you can use anything in my comments as the basis of a post. I love being part of this discussion.
I also totally agree with your points on our capacity for after-the-fact rationalization and self-delusion.
And clearly I am very susceptible to it myself. I really like your work on “thinking about thinking” and on the primary sources research methodology. And one thing you said really hit home. Like most people, my thinking and research methodology is “ad hoc and subject to extreme bias.” I know more than the average normie because I am open-minded, skeptical, and reasonably intelligent. And because once you see through a few hoaxes the rest of them become more obvious. But it is NOT the case that my research methodology is systematic. I trust my own ability to “discern” truth or falsehood much more than is justified.
So your encouragement to “think about thinking” is really great and important. And since are naturally prone to a lot of human bias, we have to think about our thinking on an ongoing basis.
I regret to have to make this post but I have come across compelling evidence that makes the case for ancient history and that civilization is as old as we are told by mainstream historians. We can finally put the history hoax to bed all thanks to bread crumbs. I can’t believe for a moment that I ever doubted ancient history but rest assured as a regular baker of bread I can vouch for the fact that this evidence is the real deal.
https://www.npr.org/sections/thesalt/2018/07/24/631583427/14-000-year-old-piece-of-bread-rewrites-the-history-of-baking-and-farming
Even the world’s leading skeptic like agent John Lebon could not possibly doubt the claims made in this article. What do you have to say for yourself now JLB?
Lol. That has to be one of the funniest articles I’ve ever read!
Thank you for posting that much appreciated comic relief.
What the hell is a paleobotanist? Plants break down in like 30 days. Lol
Chris I think that you need to take this article a little more seriously. For months now I have suspected that TPWRTS can be traced back to the oldest and most secret society of all…….the secret order of the Natufians who were well know bread worshipers. If we don’t oppose them and expose their evil intentions they will soon fulfill their agenda of taking over all of the bakeries of the world. Thank goodness for the brave paleobotanist heroes out there doing this kind of ground breaking research!
Logged on for the first time today after listening to your interview on The Higherside Chats.
I have always wondered about sources for translations but was too lazy to look (or too caught up in other things to bother, rather).
The first time I encountered an argument similar to the one you have made above was when I attended an Alpha Course as part as becoming confirmed at a happy-clappy CofE church. (Long story – I thought I was getting the Church of CS Lewis, but got the Church of What’s Happening Now.)
Anyway, the authors of the course cited counter-arguments to the common arguments against the historicity of Jesus (i.e., lack of primary sources, lack of contemporary accounts, etc.) Their counter-argument pointed out that if that was the measuring stick for the believability of any historical figures, then there was more proof for the existence of Jesus than there was for any other characters from the ancient world – such as Socrates, Plato, and even Julius Caesar – as there are more secondary sources available for the existence of Jesus than there are for most of what we “know” from the ancient world.
FWIW, I found most of the “logic” of the Alpha Course very circular, but came away with that little nugget, and in turn, it is part of what makes me open to your argument above. Recently, I read The Mecca Mystery by Peter Townsend, which calls into question the existence of a historical figure named Mohammed based on the complete lack of primary or contemporary sources, other than a Koran which was put together in “final” form in 1924, despite what we’ve been told by the History(tm) community and the media.
I am enjoying your site immensely.
Thanks for the kind words, AR, and welcome to the site.
Your comment here came up for discussion in our Member Discord call. As I explained to my interlocutors, I happen to know a man who reveres the character known as Caesar. He even helps to produce a podcast dedicated to the topic. Long story short, this gentleman is also a devout and dogmatic atheist, who believes Jesus is a myth.
Need I say more?
This fellow, friendly as he may be, is yet another case study in how humans have an almost-supernatural ability to engage in what Orwell labeled ‘doublethink’.
It would be interesting to fund out whether or not your CofE compadres could open their mind to the possibility that Caesar is a hoax. Imagine that: a simultaneous belief that Jesus was a real man but Caesar was not.
Of course, this would merely be the inverse of the Caesar believer I mentioned above. Two sides of the same coin, as it were.
I look forward to hearing more of your feedback as you check out the material in the back-catalogue.
This is a well written and researched article, it is also the reason why I purchased a full membership. I look forward to reading more of your work.
Thank you very much, Chris 🙂
It will be interesting to read the feedback of yourself and the other newer members once you have had time to check out more of the material on this site.
I comment on the Oxyrhynchus Papyri being found at a rubbish dump around 1898. In our “modern society” a rubbish dump is nothing exceptional. This is mainly because our society produces so much rubbish. I question if there existed any rubbish dumps in Egypt around 1900 at all.
Self-sustaining societies do not even tend to produce rubbish. Everything is reused or cycled back to nature. I list some examples:
*) organic waste is put back to nature,
*) cloth is repaired as often as possible; afterwards it can be used as cleaning rag; afterwards it can still be used to light a fire or put back to nature,
*) metal waste is likely collected and remelted,
*) paper/papyrus which is no longer needed can be used as toilet paper.
I can imagine that rubbish dumps existed around 1900 in industrial centers and big cities. But I believe the main part of society was still organized in an autarkic way. At least in my home Austria people tell/write that in the countryside this was the way they (or at least their parents) lived in their childhood. I don’t think anybody considers Egypt around 1900 to be an industrialized country.
I think the Oxyrhynchus Papyri should be put back where they came from – the rubbish dump.
I have read, and studied The History Hoax – A Primer, The history of ‘History’, and the history of ‘Histories’, twice.
If I trace your argument correctly, it goes like:
1) History as a distinct academic discipline is less than 200-300 years old.
2) The two primary sources on the wikipedia page for Herodotus Histories both trace back to Godley’s translation.
3) Godley’s translation is based on Stein’s translation. You can’t determine if Stein’s translation uses a primary source because it is in German (but you do point out that you wouldn’t be surprised if its source is just another translation, or if it doesn’t even list a source.)
4) The wikipedia page and Oxford itself says that the evidence for Herodotus’s Histories is a papyri disocvered 120 years ago in a rubbish heap in Egypt.
Therefore, ancient history is make believe/a sham.
There are some problems with your logic here.
1) It relies on an assumption that all evidence that can be found is available/referred to on the Internet. But, Wikipedia and, more generally, all content available on the internet, is “open source” meaning anyone can put stuff up there or not, as they wish. And there is much less motive to put hundreds year old content and related info online considering most people who actually study it do so in universities, where the information is available. So, you are using the internet and it’s contents as your only source of evidence, but you don’t know how much of the relevant evidence is available/represented on the internet. There is much more written material in the world than is on the internet. Ask Google! They are trying to scan them all, but they are reportedly not even close. “As of October 2015, the number of scanned book titles was over 25 million, but the scanning process has slowed down in American academic libraries. Google estimated in 2010 that there were about 130 million distinct titles in the world, and stated that it intended to scan all of them.” (link: https://en.wikipedia.org/wiki/Google_Books) So, google books, which holds the most scanned books available online estimates that they have scanned apx 19% of all available, published books.
2) You have only shown that “there is spotty evidence available on the internet for primary sources related to Herodotus”. That is all you have shown. But you jump from that to “ancient history is all make believe” and start throwing around “history hoax” and “sham”. Firstly, you are not even defining what hoax or sham would MEAN in this context, that in itself is a major problem, a gap in the logic. That gap leaves your audience is left to infer what you mean by referring to the shared definitions of those words. One reasonable interpretation would be that you mean: People, professors, universities, etc. are professing and/or making up stories without actual evidence. Secondly, “ancient history is make believe / a sham / a hoax” does not follow from ” there is spotty evidence available on the internet for primary sources related to Herodotus “. There are other possible explanations, like #1 above.
3) Also, the Stein translation that is in German: You can’t just find a trail, NOT follow it, and still draw conclusions/speculate about what wouldn’t be surprised by.
Lastly, here is a good example of where I think your writing is misleading and would incline honest/serious thinkers to not trust you. You wrote and published: “‘Ancient history’ is all make believe. It never happened. Or, at least, the ‘evidence’ on which these stories are based is incredibly recent and entirely unconvincing.” You can’t say “It never happened.” and you really should take that out if you want people to think you’re an honest thinker/writer. You haven’t proven that, period. You’re the one talking about evidence, what evidence do you have that “it” never happened — and also, what “it” are you talking about?” So, the fact that you have that in that sentence is very disappointing. PERHAPS you’ve proven a variation of the second claim in that sentence: “the ‘evidence’ on which these stories are based is incredibly recent and entirely unconvincing” — I’d say you could claim a variation something like: the evidence available ON THE INTERNET for primary sources related to Herodotus is spotty/hard to track. That is quite different from either the first or the second claim in that sentence.
I appreciate the work you do to encourage people to think about why they think they know what they think they know, I really do. But this kind of provocative over objective writing makes you hard to trust. Perhaps people whose current opinions incline them to want to believe your inferences/conclusions might be satisfied, but that is wishful thinking, not critical thinking, which you ostensibly advocate for.
I’m a week or two behind on replying to comments but I wanted to reply to this one asap because you are a new Member and I can see that you have taken a lot of time to read through my material before critiquing it, which I appreciate.
Firstly, you are correct that I have not ‘proven’ that ‘history’ is a HOAX. I would go further and suggest that in all of my work, I have never ‘proven’ anything, and even if I wanted to, I could not ‘prove’ that ‘two’ ‘plus’ ‘two’ ‘equals’ ‘four’. At the heart of the matter are concepts related to epistemology (what is ‘knowledge’) and metaphysics (what ‘is’). For these reasons I usually try to avoid using the term ‘prove’, but may occasionally slip into old/bad habits, and you are right to point them out so thank you.
I am confident that in at least one of the History Hoax articles I explained all of this, and made it clear that my method is based on inferences rather than ‘proof’, but perhaps I might be well served to add such an addendum/caveat to the end of every relevant article/post.
With that said, ‘prove’ can be and often is used interchangeably with ‘demonstrate’ and other similar terms, and in a broad sense, I have indeed demonstrated that ‘History’ as we are taught it (or as it is commonly understood) is in fact a sham, a ruse, a deception, a hoax. ‘History’ is not backed by the evidence which many of us seem to assume must exist i.e. primary sources. ‘History’ is not even taught to students with such evidence. ‘History’, as an academic discipline, does not exist in the way which many of us seem to believe (whether consciously or subconsciously) that it must.
What I have done is present the evidence and logic which leads me to conclude that ‘History’ is in fact a HOAX. It is important to understand the distinction here: I have presented the evidence and logic which leads me to my conclusion. But it is only my conclusion, and it does not ‘prove’ that my conclusion is ‘objectively true’. I make these presentations so those who are interested to do so, can inspect the evidence and logic for themselves, and point out any flaws or errors if they find them, but more importantly, use it as a mirror to reflect on their own evidence and logic, to reconsider why or how they arrived at their own conclusions.
In other words, if anybody reads my work on the History Hoax through the prism of ‘it is this guy’s job to convince me to believe what he believes,’ then they have misunderstood my intention (which may be their fault, or it may be mine, or a combination of the two). My intention is to share the research I have done and to encourage others to do their own research, too — and hopefully present it for the rest of us to inspect in a collegiate fashion.
Secondly, you are correct that my research is heavily reliant on the internet. If a book has not been digitised and made available on the Internet Archive (or other website) then I simply do not have access to it. This is because I cannot realistically inspect every library on earth for myself, let alone every basement/attic/storage/etc where rare books may in theory exist.
My conclusions are based on an overt and already-explained system of inference: I am inferring that the apparent absence of primary sources for characters like Herodotus (for one example) is due to the non-existence of primary sources. There may in fact be primary sources for Herodotus laying around somewhere, unseen by modern computer scanners. But why would I assume this to be the case? If others want to work on that assumption then that is their business, by the way, and it is not my job to convince them to stop working on that assumption.
I am willing to publicly state and explain my conclusions based on my own inferences, because I have taken the time to look for the primary sources and found nothing — and I have documented the process for others to see. This is not a case of ‘I demand that other people show me evidence for Herodotus’, it is a case of, ‘I went looking for myself and here is what I found i.e. nothing’.
I have also made it clear that if anybody can find the primary sources, and present this evidence to me, then I will be more than happy to inspect it, and reconsider my conclusion if the new evidence contradicts my existing conclusion. It is conspicuous that in your detailed reply here, you have not actually presented any such evidence. You haven’t even tried. Do you believe the primary sources to exist? Are you able to present evidence which supports your belief?
It is one thing to critique the evidence-logic-conclusion presentation I have made, it is another thing to make your own evidence-logic-conclusion presentation. Do you plan to do this? If not, why not?
You will not find a better platform for discussion of these kinds of matters than johnlebon.com. Period.
You have nothing whatsoever to fear from presenting your own case, your own evidence-logic-conclusion research and thinking patterns. Even if your conclusions are different to my own. You might even find that some of the Members of the site would dearly love to see a calm and logical counterpoint to my own conclusions. I have encouraged other Members in the past to present the ‘alternative hypothesis’ to my work, but sadly this has led in at least one instance to ad hominem critique of ‘John le Bon’ rather than any presentation of evidence-logic-conclusions which contradict my own work.
Each and every time my critics (be they benevolent or malevolent in intent) focus on ‘John le Bon’ rather than presenting their own case, their own evidence, their own logic; each and every time they fail to present the primary sources which I am stating do not exist; each and every time they do this, the strength of my own case is made more clear by implication.
And I love it.
Welcome to the site and I hope you enjoy your stay here. And thank you for taking the time to engage with my work before critiquing it.
Jlb is wicked smart
👌
How could there be evidence of something not happening?
It is impossible to “prove” a negative
I suspect somebody else is about to take a trip to Tucson lol.
I hope so. A trip to Tucson is the only way to truly see the wire frame mesh.
JLB,
Thanks for the quick, detailed reply.
Your “ancient history is a hoax” argument is an inductive argument. The definition/requirements of an “inductively sound” argument are: If all the premises are true, then it is very probable that the conclusion is true.
Again, if I trace your argument correctly, it goes like:
1) History as a distinct academic discipline is less than 200-300 years old.
2) The two primary sources on the wikipedia page for Herodotus Histories both trace back to Godley’s translation.
3) Godley’s translation is based on Stein’s translation. You can’t determine if Stein’s translation uses a primary source because it is in German (but you do point out that you wouldn’t be surprised if its source is just another translation, or if it doesn’t even list a source.)
4) The wikipedia page and Oxford itself says that the evidence for Herodotus’s Histories is a papyri disocvered 120 years ago in a rubbish heap in Egypt.
Therefore, ancient history is make believe/a sham.
This conclusion is not very probable given these four stated premises. Mainly, your conclusion is too broad for the premises. The conclusion needs to be more specific or more premises are required. Hence, this argument has not demonstrated that history is a hoax, as you say it has.
Because your research has only covered a relatively small portion of all possible sources of evidence, your argument structure is similar to:
1) There are reports of U.S citizens seeing alligators.
2) I searched high and low in the state of Alaska and didn’t spot a single alligator.
Therefore, alligators don’t exist in the U.S. Further: the reports are a hoax.
That would clearly not be a valid inference. All one could say is “I didn’t find any alligators in Alaska” or possibly “It’s highly improbable that there are any alligators in Alaska.”
Re: “You haven’t even tried. Do you believe the primary sources to exist? Are you able to present evidence which supports your belief? . .It is one thing to critique the evidence-logic-conclusion presentation I have made, it is another thing to make your own evidence-logic-conclusion presentation. Do you plan to do this? If not, why not?” I don’t have a belief about the validity of the ancient history stories we’re told. I’m agnostic about it because I don’t have enough evidence one way or the other, and I think that’s probably the most honest opinion someone can have on this topic. Why? Because, as you yourself said “I cannot realistically inspect every library on earth for myself, let alone every basement/attic/storage/etc where rare books may in theory exist.” Well, if that’s the only way to be sure there are no primary sources, then all of us who cannot search all possible sources would need to be agnostic about it, given the definition of sound inference.
Re: “Each and every time my critics (be they benevolent or malevolent in intent) focus on ‘John le Bon’ rather than presenting their own case, their own evidence, their own logic; each and every time they fail to present the primary sources which I am stating do not exist; each and every time they do this, the strength of my own case is made more clear by implication.” This isn’t relevent to our discussion because I am not focusing on you, I’m focusing on your argument. Using the alligators example, if there were people inhabiting another planet who knew that the U.S. was comprised of more than Alaska but they were unable to visit the states for themselves do their own search and provide evidence, they could still validly argue that an inference from “I didn’t find any alligators in Alaska” to “Therefore, alligators don’t exist in the U.S. Further: the reports are a hoax.” is not inductively sound. In this imaginary example, the invalid argument is not made more valid becasue the people who point out the unsound inference do not have counter evidence. Likewise in this case, your inference is invalid because it is not very probable based only on the stated premises you provided whether I have, or anyone has, counter evidence or not.
When I was a little boy I knew a boy that said he owned “machine guns”. I asked to see his “machine guns”, but alas, they were at his uncles. I was incredibly interested in firearms at the time, and so I pressured him into arranging a time where I could inspect and admire his “machine guns”. Sigh, no matter how hard I tried, I was never able to lay my eyes on that 12 year old’s machine guns.
@coffeebean Do you have some ancient primary sources? Tbh, I would really like to see some.
If I was a defendent on trial, and you were the DA, and I testified that 6000 years ago never happened, 6000 years ago isnt simply unknown, 6000 years ago is as make believe as 🎅, what would be your counter argument? What would be your evidence?
Nate,
Are you certain that “coffeebean” believes that “6000 years ago” happened?
He/she said,
“I don’t have a belief about the validity of the ancient history stories we’re told. I’m agnostic about it because I don’t have enough evidence one way or the other, and I think that’s probably the most honest opinion someone can have on this topic.”
It seems to me that the discussion is about the logic of JLB’s argument, not the belief (or lack of belief) in ancient history.
I guess i interpreted it the same as the outer space argument with Lesta.
In other words, coffeebean is saying that JLB hasnt PROVEN that outerspace is a hoax and so it COULD be real.
Lesta could say, “You havent proven that outer space is a hoax” and then that leaves the readers mind open to all sorts of outerspace speculation.
Seriously, what if TIME ITSELF only goes back a couple hundred years?
Everyone seems to think thats absurd, they storytell that the “records” musta got rained on for 40 days with mud or whatever
It also reminds me of jlbs article about practicing skepticism, and how realistically a skeptic must make inferences.
Excellent point and that post can be found here.
The tl;dr is that I am searching for evidence, presenting what I have found, and also making inferences based on what I have found.
These inferences are subject to change, pending the discovery of new/better evidence.
Those interested in the Outer Space Hoax discussion can find it here.
The basic gist of it is that one of the very few content creators in the ACT realm who I respect, ‘Lesta Nediam’, strongly disagreed with my position that Outer Space is in fact a HOAX.
Some people say that this disagreement was merely a clever ploy on my part, a way to create confusion among those who have worked out that Lesta = JLB.
Others say that this was Lesta Nediam’s ‘jump the shark’ moment, the point at which it became clear that Lesta needed to take a break from all of this (which he/she/it subsequently did).
Others say that this was JLB’s ‘jump the shark’ moment, the point at which I ‘went too far’, because after all, we all know there exists some place up in the sky where humans can go and just float around forever.
Well worth revisiting, especially for new Members of the site.
It seems to me that the discussion is about the logic of JLB’s argument, not the belief (or lack of belief) in ancient history
Are those two things not directly related?
I have explained why I no longer believe in ‘ancient history’, and I have presented my evidence, and my inferences from that evidence (or ‘argument’).
I am quite happy for cjo and others to challenge my position. The website could benefit from more of it: people politely challenging each others positions.
As I have explained elsewhere, though, I am presenting my evidence and offering my inferences based on the evidence.
The most productive way to challenge my position on the lack of the primary sources for characters/events of ancient history is to present those primary sources.
This isn’t happening here. It hasn’t happened in the years I have been suggesting that the primary sources do not exist.
And at this point, it seems pretty clear to me that it isn’t going to happen, because the primary sources do not exist, which is a central point of my History Hoax material.
Everything else is academic at best and sophistry at worst. The primary sources do not exist. This is far more important than ‘JLB’ or ‘JLB’s arguments’.
If somebody says to me, ‘I agree that the primary sources do not exist, but I choose to believe in ancient history anyway’, then I say, ‘well let’s agree to disagree’ 🙂
Nobody has to agree with my opinion about the reason why the primary sources do not exist. The existence of the primary sources has nothing to do with ‘JLB’ or ‘JLB’s argument’.
I am not ‘arguing’ that the primary sources do not exist. I am stating it. Until somebody comes along and presents the primary sources, I will continue to state it.
The internet is the greatest repository of knowledge the world has ever seen, unless of course you believe in the “Library of Alexandria” nonsense. Comparing it to Alaska, a US state with a very limited climate that would be completely inhospitable to alligators, is what would be called a red herring.
JLB is not strictly looking at books that have been scanned and uploaded. He is looking at stories and if an actual primary source did exist, a story would surely exist online since this is such a big part of what we are conditioned to believe. The closest thing to primary sources that exist are stories of “ancient papyri from a rubbish dump that survived thousands of years in the case of “ancient greece” and two Codices that were in the process of being burned in the case of the “bible”.
Why would you even leave open the possibility that something exists/existed that you’ve never seen evidence for? JLB is telling you where to look and there is none in the place where it should exist – i.e. the references in articles and papers on ancient history?
To compare looking for alligators in Alaska with looking for sources in the references section of articles on the subject is absurd and makes me believe that you are not a thinking person. Either that or you are just arguing to argue, which I guess has a place but I think you are projecting when you call this work dishonest.
I believe our resident German, Stansen, did look at the Stein book and determined that it too lacked any primary source(s).
The best thing for you to do would be to pick a topic older than a few hundred years old that you think has a primary source and go out and search for it. Take a trip to Tuscon. I highly doubt you will even find a believable story about a primary source, let alone something that can actually be verified. If you find something, I would be ecstatic since so much of what I thought I knew stemmed from a belief in the distant past.
Thanks for taking the time to write such a detailed comment. The website is better for it, and I can assure you that other Members of the site get something out of these sorts of back-and-forths.
I notice that you have not even tried to present any primary sources regarding ‘ancient history’. Hundreds of words and not a single primary source.
Have you looked for primary sources of ‘ancient history’? If not, why not? If so, what did you find?
As per my Practice of Skepticism post, I am not here to tell you what to believe or not believe. That is up to you.
My work is based on searching for evidence and making inferences from the evidence I have found. If you are not even trying to search for evidence, that is okay, but the words which follow from an overt disinterest in evidence are moot to me.
You can say, ‘you haven’t proven X/Y/Z’, and I will agree with you. I am presenting the evidence and reasoning which has led to my opinion. It is not my job to convince you.
In fact, as time has gone by, I have become more and more comfortable with the idea that my job as the admin of this site is to explicitly NOT convince people to my way of thinking. The more people who disagree with me, the better.
So long as the disagreements are respectful and civil, of course.
Your “ancient history is a hoax” argument is an inductive argument. The definition/requirements of an “inductively sound” argument are: If all the premises are true, then it is very probable that the conclusion is true.
Just on this, I don’t believe I have used the term ‘inductive argument’ in any of my History Hoax material. I prefer the far broader term ‘inference’ (and for good reason).
Therefore, when you say that my presentation is ‘X’ or ‘Y’, with technical definitions such as ‘inductive argument’, it is useful to explain where these technical definitions come from, and why you believe they are relevant/beneficial to conversation at hand.
If you would like to tell me where you got your definitions/rules of ‘inductive argument’ then I would be interested to read and learn more.
In fact, I am tempted to open a dedicated discussion thread on these sorts of topics/ideas (e.g. academic logic, epistemology, etc).
I would dearly love for somebody to be able to present and defend the idea that ‘inductive’ and ‘deductive’ arguments are truly distinct from one another, and that both are more than mere abstractions, and that both are more than merely subjective assessments. I once tried this myself and failed, which is why I now prefer the more broad and general term ‘inference’ to describe my process of moving from premises/evidence to conclusion.
It’s a little disappointing that you and Nate keep pointing out that I have not presented (or tried to) any primary sources, for two reasons: 1) I have explained the reasons I have not repeatedly, and having that go unheard makes me wonder if you’re not reading what I’m saying closely, or you’re ignoring what you want to ignore for your own purposes. 2) More importantly: it is perfectly acceptable to criticize an argument without having a counter argument. They are independent. So I’m not sure why you keep going back to that.
Further, to assume that your conclusion is correct because no one else has proven it wrong/provided evidence of primary sources is a fallacy. It is called an Argument from Ignorance. Description: The assumption of a conclusion or fact based primarily on lack of evidence to the contrary. Usually best described by, “absence of evidence is not evidence of absence.” https://www.logicallyfallacious.com/tools/lp/Bo/LogicalFallacies/56/Argument-from-Ignorance
However, since you kept pressing on the issue, this morning I thought, OK, Stein’s translation might have a reference to a primary source. Maybe I can find someone who knows German. Or maybe I can just contact the guy, assuming he is alive. 5-10 minutes of research led me to this english version of Stein’s: https://www.amazon.com/Herodotos-Herodotus/dp/1340598507. It is simply called Herodotus (not Herodotus’ Histories), but I assume it is the Histories because it’s apx 750 pages and because of this description: “This work was reproduced from the original artifact, and remains as true to the original work as possible. Therefore, you will see the original copyright references, library stamps (as most of these works have been housed in our most important libraries around the world), and other notations in the work.” The references to “library stamps (as most of these works have been housed in our most important libraries around the world)” might be useful. So I ordered it. It’s in the public domain, and can be reproduced, though I could not find a digital version. I will share photos of relevant portions.
Regarding inductive arguments and the difference between inductive and deductive: Deductive: the kind of reasoning used in mathematical proofs. In a deductive argument, if the premises are all true, then the conclusion MUST be true (not inferred). Inductive: the kind of reasoning used in statistics, probability, and empirical science. This is what you are doing. In an inductive argument, the conclusion is on a scale from weak to strong. “Conclusions reached by the inductive method are not logical necessities; no amount of inductive evidence guarantees the conclusion. This is because there is no way to know that all the possible evidence has been gathered, and that there exists no further bit of unobserved evidence that might invalidate my hypothesis.” However, though certainty is never possible in an inductive argument, in order for it to be a good/valid inductive argument, then if all the premises are true, then it is “very probable” that the conclusion is true. And again, the reason I’m stating that your conclusion is not “very probable” is, well, the main reason is that you have not covered much of the total area of possible evidence/primary sources. A couple links: http://www.butte.edu/departments/cas/tipsheets/thinking/reasoning.html, http://selfpace.uconn.edu/class/phil102/u12.pdf.
Regarding whether or not the concepts of inductive and deductive arguments are “mere abstractions”/subjective. I don’t know what you’re getting at by “mere abstractions”. Lots of words are abstractions but they are still useful. RE: subjective, they are definitely not. There are clear definitions (per the above). Cataloging the different sorts of arguments, and giving them names (abstract labels), allows us to have shared rules/guidelines about the logical, validity rules for different types of arguments, which allows us to make better arguments and spot bad ones. So, seems pretty useful to me.
More to come when I have had time to look through the book, which won’t even arrive until Friday at the earliest.
it is perfectly acceptable to criticize an argument without having a counter argument
I agree with you, it is acceptable to criticise an argument without providing a counter argument.
My question to you would be, what is your intention? What do you hope to achieve?
When I share my research, my evidence and reasoning and conclusions, my aim is to share where I am at, at this point in time. In doing so, if I have overlooked some piece of evidence, then others can assist me by providing the evidence, or pointing out the place where I can go to find it, or so on.
It might also be that my logic is faulty. for example, my premises might not lead to my conclusion, or there might be some better conclusion to arrive at, based on the evidence. But this does not appear to be your position. If I have understood you correctly, you are not offering a better conclusion based on the evidence, you are merely saying that my evidence does not definitely lead to my conclusion, because there ‘may be’ other evidence out there. In which case, I have already agreed with you. My conclusion is based on an inference. You may wish to draw a different inference, or no inference at all, that is up to you.
It is also perfectly acceptable to agree to disagree. I have presented my evidence, my reasoning, and my conclusion, and you seem to be suggesting that you disagree with my conclusion. That is fine by me 🙂
to assume that your conclusion is correct because no one else has proven it wrong/provided evidence of primary sources is a fallacy
This is not my assumption. Where did I write that?
What I am saying is that nobody has presented the primary source evidence despite my repeated requests for people like yourself to present it. Perhaps we are all just terrible at searching for the evidence, all of us who have tried looking. then again, perhaps the evidence does not actually exist. The more people who take time to criticise myself (or my ‘argument’) but fail to present the primary source evidence I am searching and asking for, the more confident I will become that that the evidence in question does not exist.
You may not like my confidence on this matter — that is entirely up to you — but whether or not you like my confidence on the matter, it will grow with every reply you take the time to write but fail to present the very evidence I am searching and asking for.
So I ordered it. It’s in the public domain, and can be reproduced, though I could not find a digital version. I will share photos of relevant portions.
Excellent, thank you, I look forward to it.
Regarding inductive arguments and the difference between inductive and deductive: Deductive: the kind of reasoning used in mathematical proofs. In a deductive argument, if the premises are all true, then the conclusion MUST be true (not inferred).
Apart from mathematical proofs, can you think of any examples of ‘deductive arguments’? It seems to me that mathematics is itself abstract, in the sense that there is no ‘two’ or ‘three’ of something outside of the human mind/perception. No two things in the physical world can be identical (as far as I am ware), but we as humans ascribe the same identity to certain things which we determine to be alike. We may use symbols to represent abstract concepts (e.g. ‘2’) and then represent things in the physical world with those same symbols (e.g. I own ‘2’ coffee mugs), but at this point, are we not dealing with the same subjective analysis which is supposed to be the domain of ‘inductive arguments’?
I am here to learn. As I explained earlier, there is a reason why I have not released material on ‘inductive’ and ‘deductive’ arguments. I have stuck to simple concepts such as
premise -> premise -> conclusion
and
input -> process -> output
and basic logical fallacies (e.g. ‘non sequitur’) because the more I think about the ‘inductive’ vs ‘deductive’ distinction (and so much else from the field known as ‘formal logic), the more arbitrary/abstract it seems to me. I say this as somebody who studied philosophy at university level. If you are here to help assist others (including myself) understand things better, then I for one am all ears.
Take for example this explanation of ‘deductive arguments’ from Lane Community College, which is on the first result of a google search for ‘deductive argument’. What examples do they give of ‘deductive arguments’? One mathematical example, and one linguistic/nomenclature example (‘if proper noun is in proper noun…’). Again, we are dealing with abstractions: in the case of the proper nouns, is the proper noun the concept (e.g. Sweden as a ‘nation’), the land mass, or something else? And who gets to decide? How am I supposed to ‘know’?
In both the mathematic example and the proper noun example, we are dealing with language: the language of mathematics and the language of English respectively. Therefore, to say that something is ‘certainly true’ or ‘guaranteed to be true’ means what exactly? That the rules of the language have been adhered to? Whose rules?
This is why the field referred to by some as ‘epistemology’ is something which has both fascinated and infuriated me. Rather than claim that I ‘know’ something in an ‘objective’ sense (i.e. independent of my own perspective), I prefer to say that I infer something to be true, with the implicit corollary being that I fully accept that it is a subjective matter. Thus I am claiming that the primary sources for ancient history do not exist, because I have spent considerable time looking for them, and I failed to find them. I will also change my mind if somebody can find the primary sources and bring them to my attention.
This is one of the reasons why I am so happy to agree to disagree. I will put my own conclusions out there, opinions which seem reasonable to me as I see it at this point in time, but I am not going to waste my time trying to convince others to agree with me.
I am however happy to take other perspectives on board, so again, if you are here to share your take on these matters in order to benefit myself and/or others, then fire away 🙂
I’ll respond more about the arguments/epistemology stuff when I have more time.
I too studied philosophy in college as well as logic and critical reasoning. I dabble in it a bit still because I find it interesting and important. (Also, a couple people have mentioned that I should try to do primary source research for anything older than 200-300 years ago. I also did that in college. I researched the 17th century Massachusetts Bay Puritans, and one of the primary sources I used was a book called The Marrow Of Theology, published in 1642. (It’s a rough read! but here’s a link: http://www.apuritansmind.com/puritan-favorites/william-ames/the-marrow-of-theology-online-by-william-ames-1576-1633/)
I just mainly wanted to respond to “what is your intention? What do you hope to achieve?”
Firstly, I have no interest in ancient history. Zero. I have no attachment to whether it was as we have been taught. And, I’m not so naive as to believe that history is some perfect account, or that corruption and general human fallibility hasn’t influenced both the academic discipline of history and the stories we hear and circulate.
My intention with these posts has to do with the question: what makes an inference sound? As I have mentioned, I think your conclusion that ancient history is a hoax is too broad for your premises. I think you could fairly infer “there is spotty information available on the internet for Herodotus’ histories”. That would be a sound inference because your evidence makes it very probable. But the jump from that to ‘ancient history IS a hoax’ is an extremely large jump, and is not justified by your premises. You say “My conclusion is based on an inference. You may wish to draw a different inference, or no inference at all, that is up to you.” There are guidelines about what a valid/strong inference is and, for the reasons I have explained, I don’t think your inference is valid/strong. And I think it is important that the answer to whether an inference is valid/strong should not be subjective (hence the guidelines). So, while people may indeed wish to draw whatever inferences they want (of course they do, that’s easy), I would argue that their inferences should be bound by these guidelines in order to have the best chance of being accurate/true and, therefore, useful.
OK, fine, but why do I care. Unsound/weak inferences, especially when they are not qualified as an opinion, cause harm. If everywhere you have written “ancient history is a hoax” you instead wrote “I believe ancient history is a hoax” I would never have said a word. But when people state unsound/weak inferences as facts, that causes harm. More than each instance causing harm, the habit causes much harm. You’re a skeptic, no one needs to tell you about how quickly people believe things they don’t have enough evidence for, and how harmful that can be.
Here’s one historical example that comes to mind. I’m sure you’ve heard of the Hungarian doctor Ignaz Semmelweis who figured out that doctors should wash their hands instead of inferring that illness was caused by bad air or evil spirits. https://www.npr.org/sections/health-shots/2015/01/12/375663920/the-doctor-who-championed-hand-washing-and-saved-women-s-lives That is an example where, asking the question “is the conclusion that illness is caused by bad air or evil spirits very probable“? was essential and the people inferring that it was caused by bad air and/or evil spirits were actually causing harm (unintentionally, I’m sure).
Another current example is that many, many people in the tech industry infer that women are either less able or less interested in technical roles. They cite what they believe is evidence and then infer that the reason there are few women in tech is due to something in the nature of women. Examples of these arguments are all over the place, but they’re largely slapdash arguments that don’t take into account all possible explanations. In this case, the harm is employment discrimination, inequality at work for the women who are in tech roles, etc.
Then there are the every day examples that damage relationships. People gathering “evidence” about people, say, observing their behavior and then incorrectly inferring what kind of person they are. “Tom is a bad father because he doesn’t take his children to church and let’s them eat ice cream for dinner.” Or “My husband doesn’t love me because he x, y, z.” Or, one that I’ve seen here, about me: someone saying that they think I’m not a thinking person or am here to make trouble because they had a problem with my alligators/Alaska analogy. (I am a thinking person and am not here to cause trouble.)
People making unsound inferences is a real problem, and I point it out whenever I see it.
Anyway, like I said, I’ll send more about the arguments/epistemology stuff later, probably along with anything interesting from the book. Might take a few weeks. Thanks for the respectful way you have engaged.
Regarding ‘The Marrow of Theology’, how old was the copy you studied, and how did you check its purported provenance?
There are guidelines about what a valid/strong inference is and, for the reasons I have explained, I don’t think your inference is valid/strong.
Whose guidelines?
And regardless of whose guideliness you are following, we can agree to disagree about my own inference(s) 🙂
The important point is that we seem to agree about the non-existence of the primary sources.
I think it is important that the answer to whether an inference is valid/strong should not be subjective
This is why I look forward to you (and anybody else) taking the time to give real-world examples of ‘deductive arguments’.
If there is conveyable ‘truth’ in this world which is not, ultimately, a matter of subjective interpretation, of human expression, then it will come as a revelation to me.
Unsound/weak inferences, especially when they are not qualified as an opinion, cause harm
I suspected this might be your motivation, thank you for your honesty. This tends to be the case: those who want to argue with my conclusions, despite being unable to offer counter evidence, tend to view themselves as saviors of some kind, defenders of the little guys, protectors of the people who can’t protect themselves from JLB and his radical research. I’ve seen it before and I will see it again.
How can somebody be ‘harmed’ by letting go of belief in ‘Ancient History’? Serious question. What ‘harm’ can come to those who make similar inferences to my own regarding the lack of primary sources concerning characters like Herodotus?
What relationship was damaged or harm done? If I don’t think you’re a thinking person or are here to cause trouble due to your spouting ridiculous analogies, how have you been harmed?
Do you see how looking for alligators in a place with a climate completely inhospitable to their biology should not be compared to scouring the internet (the greatest repository of human knowledge the world has ever known) for primary sources in articles where they should exist?
Do you dispute that this is, in fact, a red herring?
If you were trained in logic but chose to present a red herring, in my opinion (I thought it was obvious that when someone was writing/ speaking they are expressing their opinion), you are here to cause trouble.
Yes, I do dispute that it is a red herring. The two reasons I thought the analogy was fair/useful are below. Also, I’ve already articulated both of these things, before I made the analogy. My hope was that people would be able to follow the reasoning.
The content on the internet is open source, so to speak. I don’t know why you say any content “should” exist on the internet. Like, we’re entitled to all content in the world being available? Content that is made available on the internet is usually/mostly done so as a result of demand (economic or otherwise). How many people are interested in being able to see primary sources related to Herodotus on the internet? I would guess that most people who would want that are associated with a university, and would be using university libraries/resources.
Just because the internet is the largest single repository of knowledge doesn’t mean all books are available on it. Did you see the Google Books statistics? They are trying to get as much content posted as possible, and they have been working on it for years, and they estimate that they have scanned 19% of all books.
So, if we take “81% of published books (not to mention unpublished books) are not available on the internet” along with “ancient, obscure material that very few people are interested in, and most of those that are will be studying in universities” then the internet is inhospitable analogy isn’t ridiculous.
After making this analogy you call ridiculous, I then found the English version of Stein’s work, which has this printed on the back: “Therefore, you will see the original copyright references, library stamps (as most of these works have been housed in our most important libraries around the world), and other notations in the work.” Note the reference to library stamps, not URLs.
But rather than being charitable, you went to thinking I was not a “thinking” person or was trying to cause trouble. It’s interesting that you didn’t ASK me why I thought the analogy was fair. I mean, seriously, if it seemed to not make sense to you, why not ask me to explain my reasoning? Although/further, as I said above, I already had articulated these reasons.
In any case, I do not find JLB or this community to be truly skeptical or open-minded. These responses are full of “true believer” thinking, not skeptical thinking. So, I will not be sticking around.
If anyone is interested in the English version of Stein’s work, with the library stamps, etc., it’s available on Amazon at the link that follows. It’s in the public domain, so it’s possible it’s on the internet somewhere but I didn’t find it. I suppose I could upload it myself to contribute to the “largest repository of knowledge” but it’s 750 pages and I don’t have a public website, nor want to pay for one for this purpose. Hmm, guess we’ll have to wait for someone to have some motivation to make this information available to the public. Until then: “ancient history is a HOAX”! Hooray for weak inferences! Hooray for believing whatever we want in the name of skepticism. Have fun in the true believer JLB club.
Link to book: https://www.amazon.com/gp/product/1340598507/ref=oh_aui_detailpage_o05_s00?ie=UTF8&psc=1
When I said the references “should” be there I was not claiming that I am entitled to this information. I’m saying that an article about a figure from ancient history should reference a primary source. Instead, what we find is references to secondary and tertiary sources at best. What you did there was present a strawman argument.
Maybe you really are not very intelligent. You can’t see how looking for an animal in a climate where it cannot exist is not even in the same ballpark (not even the same sport) as looking for sources in online articles and journals that are supposed to cite sources. Every scholarly article/paper is required to cite sources. Alligators can’t live in Alaska. See the difference?
Your link to an amazon listing of Stein’s book is not a primary source or anything even close to it.
You keep referencing books. I’m not talking about books. This is called cherry picking. I’m talking about papers and articles, those papers and articles on subjects of history reference books, those books reference . . . nothing or each other.
I am no true believer. I have gone searching for sources and have found none. Not in libraries, the internet, or rare bookstores.
If you just take the time to read the comments on this page, you will see that Stansen, a native of Germany, left a comment on 10/27/17 saying that the Stein book does not cite any primary source(s).
I highly doubt you actually ordered the book as you seem to be the SJW type who like to throw peanuts from the gallery but don’t actually want to do any work.
I really wish you would stick around and debate this. Maybe even find us one of those books that must exist yet noone can manage to find. Maybe you’ll be the first. I doubt it though.
I know, I know, you don’t have to present a counter argument to criticize someone else’s argument but it seems silly to me.
I understand about inferences. But there are limits to what is considered a valid/fair inference. You can’t just make any inference you want. (I’m not saying JLB is doing that at all, he clearly is not.) Re: valid inferences, that is where the definition of “inductively sound” comes in, and I went into a lot of relevant detail about it in my last post.
Is it fairer to infer that 6000 years ago DID occur, or is it fairer to assume that 6000 years ago DID NOT happen?
Yeah, yeah. Nobody has an opinion either way 😉
They say there are no athiests in fox holes. (Lol, my keyboard just tried to correct “holes” into “jokes”)
@coffeebean If someone held a gun to your head and asked you if “things actually occurred” 6000 years ago, what would you say? Yes, yeah?
Maybe im wrong, but sometimes I think conscious minds hide behind the shield of “you never know”
I would say I don’t know because I don’t. If they asked me what I believe, I would say I don’t have a belief, nor do I feel a need/compulsion to have a belief/story about it.
Also, I already explained this in the post you seem to be responding to. I wrote: “I don’t have a belief about the validity of the ancient history stories we’re told. I’m agnostic about it because I don’t have enough evidence one way or the other, and I think that’s probably the most honest opinion someone can have on this topic. Why? Because, as you yourself said “I cannot realistically inspect every library on earth for myself, let alone every basement/attic/storage/etc where rare books may in theory exist.” Well, if that’s the only way to be sure there are no primary sources, then all of us who cannot search all possible sources would need to be agnostic about it, given the definition of sound inference.”
I’m beginning to wonder if you read it. Maybe that is not the post you are responding to?
Re: the atheist in fox holes comment, I have no idea what you’re talking about or how it is relevant to this discussion. Feel free to enlighten me on that.
Yeah, im drinking, probably reading between the lines.
I suppose im calling the “agnostic” bluff, i dont think real life people function on a foundation of “idk”, they may say they do, they may think they do, but it seems far fetched to me.
Thinking that the past only goes back a couple hundred years is a revolutionary idea.
Its understandable that even the most monk like skeptic would have some “misgivings” to that inference.
@all Do you have any misgivings to that inference?
We can dream about ancient cataclysms and billions of years of evolution, because that is possible until PROVEN WRONG, or we can instantly drop all those empty stories like a bag of dirt.
But you say, “dont drop that bag, you never know…”
Thats how i was seeing it
@coffeebean
Arent you being unrealistic? If someone held a gun to your head and demanded an A or B answer, you would refuse and fight them like a smart ass?
Cmon…..
Really? Thats fine. You dont know what you believe. Someone hands you a roman coin and you are like a new washed babe, no programmed thoughts percolate to the surface when you grab that coin. Respect 👊
Btw coffeebean, Im not attacking you. I hope you dont see it like that.
The questions you are expressing are what that I, and probably many of the other members, have had bouncing around our noggins for quite some time.
Im not your enemy, far from it.
Sometimes I play devils advocate, and sometimes I pretend like certain things are serious, but seriously, Im glad an intelligible pov has appeared on this site.
Welcome! Cheers bro!
My comment about foxholes…
My interpretation of that quote has changed over the years.
I used to think that people in foxholes were desperate to believe in anything, they would believe in pink elephants if it got them out of that predicament.
Nowadays, I think of the quote as a nod to the idea that when the “shit goes down” we shirk the pageantries and dive open armed towards our foundational beliefs.
But usually most jlb followers play like they dont know what they believe. I CALL BULLSHIT
FWIW, I am open to the History is Hoax argument, but I don’t think it is all a sham. I do think what comes down to us as “History” is controlled and flavoured by the powers that be: “History is written by the assassins” as Sherman Skolnick used to say.
I shared some of the thinking on this topic with my wife. She studied paper conservation at college in the mid 90s. She can assure me that she has seen acres and acres of records and books kept in underground, climate controlled environments in the City of London, Edinburgh, and at the Victoria and Albert Museum. At the time, these institutions used the handful of students studying paper conservation (maybe 30 or so per year) to help them catalogue what was in the collections during their work experience weeks – and it was a painstaking process for each document or book they handled. And they had to already be trained in the proper handling of fragile paper artefacts.
There was so much in those collections that is uncatalogued, that she doubts they are anywhere near completing cataloguing. And many of the manuscripts are so fragile, she doubts they will ever get around to digitising them.
She also said that if there was something you wanted access to in the V&A which was catalogued, it could take up to two hours for them to emerge with the item, and only after you had been vetted in knowing how to handle the documents you were entrusted with.
There is a lot of information which may never make it to the internet in digital form and relies upon free labour of college students to sporadically maintain.
How old did “they” (the people running these facilities) claim the books and documents are/were? How did they go about confirming the age? What was the chain of custody/provenance?
My position is that a book from the mid 1800s would need to be preserved in vaults like your wife described for it to be readable now.
The oldest book I have ever laid a hand on was from from the late 1800s and it was falling apart. It had been stored in a climate and humidity controlled environment since the mid twentieth century.
I don’t believe that any document could survive a thousand (or even more than a couple of hundred) years and stories that claim they have are absurd to me.
Can your wife tell you how long a written document can survive even when preserved using the technology of today? I’m genuinely curious.
The other issue is that none of these references cited in papers or books that I’ve found cite any such documents or books. Are we to assume that they had access to these vaults but didn’t bother referencing the sources?
I’ll have to ask her at an opportune time.
She thinks I’m in the office watching porn. Can’t let her know what I’m doing here. 🙂
Hey Nate, I know what I believe, that history started just a couple of hundred years ago. I tracked the Vikings back to 1795 and that is where their story starts. The bible has also received my attention, this goes back to 1839 when Queen Victoria registered her patent/copyright. I’m going to keep looking at different historical normie beliefs until I am blue in my face. I’m currently checking out Napoleon Bonaparte as he is sited as existing in the time when we all seem to appear from the aether. What a strange place we live in, where people exhibit extreme cognitive dissonance, fighting their own ego’s to hold onto unfounded beliefs.
For most of my life I have had visions that the past is not real. When i was a kid I thought everybody knew but we werent supposed to talk about it. When I grew up, I thought I was just plain crazy 🙁 but this history hoax stuff makes me think maybe its the truth.
“The future is certain, give us time to work it out.” Just relax your mind and see the future as coming first, and the past is a bunch of counterfeit clues we left for ourselves to help us find our way back to the future, back out of the labyrinth. Its all a joke, we are playing it on ourselves. Its the revelation that we are God.
I believe this will be the last thing I say here. I cancelled my membership earlier, but JLB made a change so that I can access still since I paid for a month.
The book arrived. Unfortunately, the listing on Amazon’s site is wrong. It is not English, it is German. Fun.
But, three days ago I posted a question about primary sources for Herodotus Histories to the history stackexchange. stackexchange is a great resource for asking questions of people who are experts or studying various topics (statistics, philosophy, history. . .) I had not looked at it again until a few minutes ago, and what do you know, several people who apparently actually study this provided a lot of good info, including the locations and dates of the surviving manuscripts. I’m including the link to the entire thread below, so you can look for yourself. Looking at the details there is better because several of the details are hyperlinks. But, here is a portion:
“For a critical discussion on how modern versions of Herodotus’ Histories have been compiled from the surviving manuscript sources, you could do a lot worse worse than the 1983 essay On Editing Herodotus by R. A. McNeal.
This includes a useful overview of the merits of the various surviving copies and partial copies of the text.
Essentially, the problem is that no totally complete manuscript of Herodotus’ Histories survives. Furthermore, none of the early manuscripts that do survive completely agree on the text (mainly due to scribal copying errors and selective editing in medieval scriptoria). The earliest surviving copy, “called ‘Codex A”, is owned by the Biblioteca Medicea Laurenziana in Florence and forms the basis for all modern translations.
The principal surviving manuscripts for Herodotus’ Histories are assigned letters. The earliest examples (dating to the 10th – 14th centuries) are:
A Florence, Laurentian 70, 3. – 10th Century CE
B ‘Codex Angelicanus’, (named for the library in Rome where it is currently held, but previously known as the Passioneus manuscript). – 11th Century CE
D Vatican graecus 2369. 11th / 12th Century CE
R Vatican graecus 123. A composite manuscriptdating to the 14th Century CE
S The “Sancroftianus” (named for its former owner, Archbishop Sancroft). 14th Century CE
U Rome, Vatican Urbinas 88. 14th Century CE
C Florence, Laurentian conventi soppressi 207. 11th Century CE
E Paris, BNF suppl. 134. (Also contains extracts of Plutarch and Diogenes Laertius). 13th Century CE
P Paris, BNF gr. 1633. 14th Century CE
and another snip:
“Going further back in time: my local uni’s library has a copy of a 1475 Latin translation, printed by Arnold Pannartz. The 1911 Britannica article on H says
The history of Herodotus has been translated by many persons and into many languages. About 1450, at the time of the revival of learning, a Latin version was made and published by Laurentius Valla. This was revised in 1537 by Heusbach, and accompanies the Greek text of Herodotus in many editions. The first complete translation into a modern language was the English one of Littlebury, published in 1737…”
Link: https://history.stackexchange.com/questions/49617/where-can-i-find-the-primary-source-for-herodotus-histories
OK, goodbye everyone! You wouldn’t want a (“maybe”, well at least you said maybe) “not very intelligent” troublemaker around anyway.
As I explained in my most recent email to you, there is no reason for you to feel unwelcome on this site, even if you choose to maintain belief in ‘ancient history’. I’m sure there are plenty of other Members of this site who still believe in Ancient Egypt, Ancient Rome, and son on. and I know for a fact that several Members of the site maintain belief in the historicity of the Bible. And none of this is any problem whatsoever.
At the risk of belaboring the point, let me say it again: it is okay to agree to disagree 🙂
Regarding your use of Stack Exchange, I commend you for looking for information on other sites, and in particular for the way you phrased your question to them in the OP of that thread. Did you personally find the response from ‘senpaiscuba’ to be compelling?
Senpaiscuba (SS) claims that the oldest version/source of Herodotus’ ‘Histories’ currently available is ‘Laurentianus 70.3’ which is also known as ‘Codex A’. It is apparently dated to the 10th century CE. The obvious question which follows is: what is the provenance of this source? Who discovered it, how did they date it, when was it first cited, and who has owned/possessed this material ever since? None of those questions are asked, let alone answered, by SS. Would you agree that these are questions worth asking before accepting as legitimate the source in question?
SS also provides images of what is implied/purported to be primary source material of Herodotus’ work, in the form of papyri fragments. These images are all from the ‘Oxyrhynchus Papyri’ which were discovered by Grenfell and Hunt in the late 1800s.
http://www.papyrology.ox.ac.uk/POxy/papyri/the_papyri.html
In other words, those fragments were ‘discovered’ about 120 years ago. In a ‘rubbish dump’. By two Oxford Scholars. Who also happened to find papyrus fragments of the works of Plato, Euclid, Sophocles, homer, and others, in the same ‘rubbish dump’.
Do you see a potential problem here? Or does this story seem believable to you?
This thread sort of reminds me of my favourite scene from 1984; O’brien’s long conversation with Winston.
When you challenge ‘History’ there are hundreds (maybe thousands) of related and intertwined beliefs that in the mind of one who believes in stories and tales, are challenged deep within their subconscious.
To challenge History is to challenge Science, Religion, family lineage, education, gender equality, racism and race mixing, war, climate change, etc ad infinitum.
This is just too much to ask, each of the few items listed above has their own dozen or more sub-beliefs which uphold their merit respectively. To actively be aware of the foundations of our beliefs and to unravel those beliefs to get to the core of everything we hold dear to our hearts, that which gives us meaning, purpose, happiness, love, hope, and knowledge, this is truly an insane thing to do. I’m not entirely sure I believe that this character trait can be taught, OR shown. It may be the case that we are born with, or without this ability and nothing that any of us do or say will ever change the foundational lines of code we are all born with.
If a sirius problem is not seen upon reaching the fact that the ‘Oxyrhynchus Papyri’ underpins… Everything…I do not think it can ever be seen. The layers upon layers upon layers of doublethink that must be rummaged through to get to clear sight, it is an unbearable and maybe even impossible task to those not born predisposed with the ability.
Don’t you see? This IS a ‘primary source’ the experts have it, and they have said that it is so, so it is as they say…
It seems to me that we have not even grazed the surface of the very first layer of programming that must be undone before one can see anything at all.
This must truly be one of the most lonely paths in all existence. What a time to be alive.
When you challenge ‘History’ there are hundreds (maybe thousands) of related and intertwined beliefs that in the mind of one who believes in stories and tales, are challenged deep within their subconscious.
This is it in a nutshell. We have been programmed with layer on top of layer on top of layer of nonsense. For a regular person to go from normal (normie) belief to a position of real skepticism is a gigantic step. It didn’t happen for me overnight and I do not expect it of anybody else. In fact it took me a couple of years to go from the Baby Hoaxes to the History Hoax. And I jumped into all of this headfirst, so I was moving through the ideas and material faster than most people can/will (due to time constraints e.g. family/career), and I was more inclined to synthesise my own ideas due to being a content creator (whereas most people will simply parse through the content without ever really thinking about what they are consuming — it is all mere entertainment in practice if you are not actively synthesising your own thoughts).
To actively be aware of the foundations of our beliefs and to unravel those beliefs to get to the core of everything we hold dear to our hearts, that which gives us meaning, purpose, happiness, love, hope, and knowledge, this is truly an insane thing to do. I’m not entirely sure I believe that this character trait can be taught, OR shown.
Insane indeed. In the past I have likened it to a form of masochism: if it is painful for humans to admit/realise that they have been fooled, then the process of serious deprogramming is one gigantic exercise in self-flagellation. Day after day, week after week, year after year, I have been learning about my own stupidity, my own ignorance. One must truly be able to overcome one’s own ego to make even trivial progress on this path.
Every new Hoax, once fully understood and internalised, is like another punch to the face of the ego. You thought you were so smart, didn’t you? I know I did. After all, I put so much time and energy into school, and I did well, I got awards and scholarships and stuff, I was RECOGNISED, god damn it…
If a sirius problem is not seen upon reaching the fact that the ‘Oxyrhynchus Papyri’ underpins… Everything…I do not think it can ever be seen.
This is something I have been trying to convey in more recent work: some people cannot see the truth. They will not see the truth because they cannot see the truth. This goes so much further than mere brainwashing or conditioning: we are talking about creatures who will only ever ‘see’ what their authorities and the group consensus tells them they can see. Humans are NOT what we were led to believe they are.
I still think there are quite a few Members of this site, some who have been here for a long time, who don’t understand how literal I am being when I say that these creatures we call humans are NOT what we were led to believe they are.
This must truly be one of the most lonely paths in all existence.
Indeed. Were it not for this website, I would feel — quite rightly — that I am truly alone. I am finding it more and more difficult (although that is not the right word) to seek conversation with the regular people. Once upon a time I was an outgoing person, I wanted to talk with people, get to know them, find out what they thought about different things. Now I just don’t feel any inclination. I know these people already. Production line humans with nary an original thought in their brainless noggins. Compounding matters is the fact that I am surrounded by them. This makes me feel even more alone, to be in the presence of thoughtless creatures. I would feel less lonely in complete solitude.
[Probably a fake quote. Most quotes on the internet are fake, in my experience. But fake or real, this resonates with me]
Re: feeling welcome, you might want to check with watermanchris on that. Seems he thinks I’m a non-thinking, “maybe not very intelligent” troublemaker.
Re: your questions about codex A and the papyri fragments discover 120 years ago, it seems you should ask these people who have at very least apparently have studied this more than you have/have access to more information than you do. They are reasonable questions (and for the record I did not accept this information as proof of anything, simply more information/leads), but you’re the one making the inference, so you’re the one who should do due diligence here by following the leads, if evidence and a strong argument/inference is what you’re after. If you will not ask, I will, but I would be curious why you wouldn’t.
As to agreeing to disagree. As I have said repeatedly, I don’t have a belief about this issue. I wouldn’t say that I disagree that history is a hoax. Nor would I say I agree. I would say, “what’s the evidence”? I did that with the argument you provided, found it to be weak, and here I am. It’s not valid to agree or disagree with a weak inference. If someone just wants to believe a weak inference, sure go ahead. But that’s faith, not reason.
OK, I asked some of your questions, JLB. I got one piece of useful information back so far:
“The literary works and works by ancient historians among them are a tiny fraction of the total number of fragments. If they only found fragments by prominent classical authors, that might have been a suspicious coincidence. Finding documents by that many authors among a giant pile of business contracts, wills, letters, and edicts is not that surprising at all.”
So, I started thinking, someone has to have written a book about the excavation. And I found two. I’m including some detail below about/from both for anyone who is interested in researching these questions further.
I won’t continue to convey information posted to your questions, but anyone else is free to look at the thread here: https://history.stackexchange.com/questions/49733/codex-a-for-herodotus-histories-and-questions-about-discovery-of-the-fragments
And with that, goodbye!
The City of the Sharp-nosed Fish, by Peter Parsons, published in 2007.
Here is the summary:
“In 1897 two Oxford archaeologists began digging a mound south of Cairo. Ten years later, they had uncovered 500,000 fragments of papyri. Shipped back to Oxford, the meticulous and scholarly work of deciphering these fragments began. It is still going on today. As well as Christian writings from totally unknown gospels and Greek poems not seen by human eyes since the fall of Rome, there are tax returns, petitions, private letters, sales documents, leases, wills and shopping lists.
What they found was the entire life of a flourishing market-town – Oxyrhynchos (the`city of the sharp-nosed fish’), – encapsulated in its waste paper. The total lack of rain in this part of Egypt had preserved the papyrus beneath the sand, as nowhere else in the Roman Empire. We hear the voices of barbers, bee-keepers and boat-makers, dyers and donkey-drivers, weavers and wine-merchants, set against the great events of late antiquity: the rise and fall of the Roman Empire and the coming of Christianity.
The result is an extraordinary and unique picture of everyday life in the Nile Valley between Alexander the Great in 300 BC and the Arab conquest a thousand years later.”
Here is the prologue.
“This book began, in a way, fifty-five years ago, when as a schoolboy I became fascinated with the strange symbols of the ancient Greek alphabet, and discovered that, with some grammar and a dictionary, it was possible to make sense of the high poetry encoded in these symbols. When I went on to follow the traditional classical course at Oxford, I found that the corpus of Greek texts was not in fact static. Works long lost were being reconstructed, in fragments, from papyri – above all, by the austere genius of the legendary papyrologist Edgar Lobel, from the great collection of papyri excavated at the ancient city of Oxyrhynchos in Egypt. In 1958, after my final examinations, I approached the then Professor of Greek, E. R. Dodds, for advice: if I was to undertake postgraduate work, what areas might be most profitable? He replied (in those unregimented days) that anything was possible; but that in the Oxford context two areas particularly needed research and the teaching that might follow from it, Papyrology and Greek Religion. I thought, rightly, that Greek religion would require more subtlety and imagination than I possessed; papyrology, on the other hand, depended in the most concrete way on the process of decoding from which I had started.
I had enthusiasm but no knowledge, and so I went to learn the elements of the trade. First, in Oxford, I had the good fortune to be taught by the Revd Dr John Barns. He was a genial and eccentric figure, who straightened papyri by sitting on them and halfway through our sessions would produce a bottle of Guinness and drink it (‘Sorry I haven’t got one for you, old man’). He was also a scholar of exceptional learning (he knew Egyptian as well as Greek) and broad interests, and under his supervision my vision widened from the familiar literary texts to a whole new world of everyday documents. For the sake of the documents, I moved on to the University of Michigan at Ann Arbor, to study with Professor Herbert C. Youtie, the world leader in the field. To him and his wife Louise (also a papyrologist) I owe a year of kindness (including the gift of ear-muffs against the bitter Michigan winter) and a paradigm of scholarship conducted in the spirit of international amity and collaboration. Youtie understood the documentary language as few others, and his intuitive gift enabled him to decipher the most illegible script and also to detect errors in the decipherments of others: I remember how he would read through newly published texts, questing like a bloodhound, and then a sudden ‘Hah’ showed that he had found a mistake and imagined the correction required. He made himself the arbiter of the subject, but without any arrogance: ‘We all stand on one another’s shoulders’, he would say.
When I returned to Oxford in 1960 I found myself teaching documentary papyrology and deciphering unpublished papyri from the Oxyrhynchos collection. This research was by then (as it remains) a team effort, under the direction of Eric Turner, Professor of Papyrology at University College London, whose organising genius gave the enterprise a more formal shape, along with institutional premises (in the Ashmolean Museum, Oxford) and the funds (from the British Academy) to appoint a curator of the rehoused collection and to carry through the first systematic cataloguing. In Oxford I had the privilege of working alongside two colleagues of extraordinary accomplishment, John Rea and Revel Coles. The Egypt Exploration Society, which had funded the original excavation, continued (and continues) to publish our results in yearly volumes of The Oxyrhynchus Papyri.
The pleasures of the project have been threefold. First, there is the pleasure of the chase: open a box of unpublished papyri, and you never know what you will find — high poetry and vulgar farce, sales and loans, wills and contracts, tax returns and government orders, private letters, shopping lists and household accounts. Then, there is the pleasure of comprehension: as you decipher the ink, still black after two thousand years, you begin to make words out of letters and then sentences out of words; the eye looks for shapes, and the mind looks for sense, and the two in alliance will (all being well) turn a string of symbols into intelligible text. Thirdly, your new text finds its place within larger structures. A fragment of Greek Comedy may add a new scene to a play already known from other fragments; an edict of the governor of Egypt may join other documents to hint at reform and politics; the lease of a vineyard will contribute evidence about price-inflation and consumer preference. Throughout the process, the researcher becomes aware of a unity. Every fragment of every kind in every box belongs in one historical and geographical context – the reading, writing and working citizens of Oxyrhynchos, the City of the Sharp-nosed Fish.
The work of publishing the papyri reached its centenary in 1998. I wrote a piece about it in TLS of 29 May 1998, and on this basis Toby Mundy commissioned the present book. His encouragement got it going; but progress was slow. As a step on the way I contributed the material for four programmes on BBC Radio 4, broadcast in May 2002, with readings by Michael Kustow: it was a great pleasure to work with the producer, Amanda Hargreaves of BBC Scotland. Still progress was slow, and it has taken all the bracing diplomacy of my long-suffering editor, Benjamin Buchan, master of the carrot and the stick, to bring the book to a conclusion. I am most grateful to all the midwives who have helped to induce delivery.
This was to be a book in which I shared my enthusiasm with the general reader. Its purpose is simply to illustrate some aspects of life in Oxyrhynchos, a Greek city in Egypt under Roman rule, from the original documents. Professional colleagues will find it sadly lacking in many aspects. It cuts corners, when it comes to technical problems; the translations of documents (my own) often choose one alternative, when other scholars have understood the text differently. It is Greek-centred, since it draws entirely on Greek documents, and male-centred, since such was the society it describes. It focuses on the initial period of Roman rule (from the first to the mid-fourth century AD), though it brings in earlier and later evidence for phenomena which represent continuing features of the landscape, but within that period overemphasises continuity against change. There will be many simple mistakes, and many failures to incorporate the latest scholarship. There would be many more but for the expert friends who so kindly read portions of the book in typescript: Revel Coles, Nick Gonis and David Thomas.
Readers who look for something less anecdotal will find an up-to-date survey, by a cohort of professionals, in the symposium Oxyrhynchus: a City and its Texts, edited by A. K. Bowman and others (London, forthcoming, 2007); more basic information, and images of the papyri themselves, on the web site Oxyrhynchus Online. Alan Bowman, Egypt after the Pharaohs (2nd edn, London, 1996), and Roger S. Bagnall, Egypt in Late Antiquity (Princeton, 1993), provide magisterial overviews of Greek Egypt; Richard Alston, The City in Roman and Byzantine Egypt (London and New York, 2002) offers rich resources of fact and argument. Even the most banal documents can, in expert hands, contribute powerfully to social and economic history; see for example Dominic Rathbone, Economic Rationalism and Rural Society in Third-century AD Egypt (Cambridge, 1991), and Jane Rowlandson, Landowners and Tenants in Roman Egypt (Oxford, 1996). Barbara Macleod encouraged the writing of this book, even in her last illness, and it is dedicated to her memory. Her friends found in her an unfailing pleasure of intelligence and vitality, affectionate empathy and practical unshowy kindness: a brave heart and a gentle hand.
Peter Parsons Oxford September 2006”
Oxyrhynchus: a City and its Texts. A more technical book on the excavation, referred to in the prologue above.
Do any of those books have pictures of the assembled papyri pieces?
https://www.google.com/search?q=sentence+made+with+refrigerator+magnets&client=ms-android-att-aio-us&prmd=sivn&source=lnms&tbm=isch&sa=X&ved=2ahUKEwjWlcKo9YTfAhVF-6wKHT1dBFUQ_AUoAnoECA4QAg&biw=360&bih=560#imgrc=S00XNxw-OxN6VM
And another thing, I would think that scanning the oldest documents would be the first priority for those librarians working in those mysterious vaults full of ancient texts.
“Jeez, no time to scan these letters penned by Christopher Columbus like I want to,I gotta make my way through all these tv guides and readers digests first”
Uuuummmm, yeah. We know the story of the magical papyri that survived thousands of years in a rubbish dump only to be “discovered” 130 years ago by a couple of Oxford scholars named Grenfell and Hunt. I just don’t see how anybody could actually believe it.
I rest my case re: thinking person
Doesn’t it seem absurd to you that papyri (primitive organic paper) could survive thousands of years underground?
Lack of rain they say? Are we to believe that over thousands of years no moisture touched these papyri? If it didn’t, why didn’t they turn to dust? If it did, why didn’t they rot? What about micro-organisms in the soil?
It boggles the mind that normies believe this nonsense but to have someone who ended up here post these ridiculous stories as some kind of evidence of ancient history? WTF?
As to agreeing to disagree. As I have said repeatedly, I don’t have a belief about this issue. I wouldn’t say that I disagree that history is a hoax. Nor would I say I agree.
Well once you develop your own opinion on the matter, then I will be happy to agree with you if you arrive at the same conclusion as myself, and I will also be happy to agree to disagree, if our conclusions are dissimilar after all 🙂
Also! I forgot to say. . if anyone wants to reply to any of the replies to my question at stackexchange, you can! Just click the link, create an account, and ask/comment away. These are great sources of information. How much you trust the information is another story/more complicated question. But, at least it’s a good source of info that you can then choose what to do with.
JLB, I wanted to answer your last comment here, but I don’t see any comments on this page anymore. What happened?
WordPress is acting up and hid all the comments . . . again.
Maybe JLB can copy and paste all the comments (there were way more than this last round) onto the forum and we can continue our discussion over there.
I know it’s a lot of work but maybe there’s an easy way to do it.
The latest member video explains what happened. Check it out.
How unfortunate.
I have a copy of your comment, JLB’s reply, and my reply to JLB safely saved on my computer. WordPress starting acting up just as I was about to post my reply, which is really unfortunate…
(Jumpy, you might want to check the forum by the way)
It is a good idea to save all of these comments to your computer, in case the guy who runs this website is, like, deleting the comments because he doesn’t have time to waste on Figure Eights 😉
It is not a “Figure Eight” to find a digitized version of a manuscript of Herodotus’ Histories written in ancient Greek that is purported to date back to the early 15th-century, that can be freely consulted online by anyone, and that has a detailed chain of provenance. Indeed, it is directly relevant to some of the claims in this article, even if it does not “prove” that Herodotus existed or that he lived 2000+ years ago.
https://www.bl.uk/manuscripts/FullDisplay.aspx?ref=Harley_MS_6312
Similarly, it is not a “Figure Eight” to find a Wikipedia page listing the locations of the manuscripts claimed to be the original sources for Caesar’s The Civil Wars, as it is directly relevant to the following claim “I have established that primary sources either do not exist (or cannot be found) in one specific example where they are claimed to exist (i.e. Caesar’s The Civil Wars)” from this article:
https://www.johnlebon.com/articles/burning-the-library-of-alexandria-part-ii/
https://fr.wikipedia.org/wiki/Commentaires_sur_la_Guerre_civile#Les_manuscrits_sources
And yes, as I wrote in one of my comments which unfortunately “disappeared”, it is fine to question the validity of the counter-evidence, as long as the same scrutiny is applied to the claims made in the article(s).
We are all well aware that wikipedia and other outlets claim that there exists books which are X years old.
The issue is whether or not we can verify the provenance or chain of custody of these texts.
You have shown no evidence of even trying to verify the purported ages for yourself. You have merely repeated the official stories.
We can keep going around in this figure eight but it will only waste my time and the time of anybody else who reads the thread.
This is why I am no longer going to approve ANY of your comments on this article. Period. I’ve wasted enough time already.
What I can offer to do for you is to publish an MC on this site, for all to read and comment upon, of your beliefs / opinions / arguments / research / evidence / whatever.
This way you get to share and discuss whatever it is you think you are providing with your commentary.
Meanwhile the comment section of my content is not polluted with your figure-eight go-nowhere rhetorical nonsense.
All you need to do is type up your beliefs / opinions / arguments / research / evidence / whatever and send it through to me as a doc or pdf file.
I will then publish it as an MC on this site asap.
You can decide if your MC is attributed to ‘MX’ or to ‘Gaia’.
If it turns out that you do in fact present actual research in your presentation, I might even engage with you in the comment section of your piece.
If instead you simply continue to parrot the official story, with no attempt at verification of the provenance of the texts, and/or continue to pretend you don’t know what the word ‘hoax’ means, then I’ll probably steer clear, but all other Members will be welcome to comment and interact with you about your work.
Cheers.
If you don’t understand the difference between stories and evidence, this probably isn’t the place for you.
The ownership/providence section of your first link is hilarious! I will paste it in full and highlight some dead giveaways to its hoax cred –
“Provenance:Inscribed on parchment fragment probably cut from earlier binding and now pasted onto f 60 ‘1449 die inc a | pralis | Herodotus Petri Mann[.] etc’. Inscribed c.1600 ‘Reverendo Misser Pauolo’ (ff 23v, 36r). Owned by the Jesuit College, Agen (f 1r; Fontes p. 48).The Harley Collection, formed by Robert Harley (b. 1661, d. 1724), 1st earl of Oxford and Mortimer, politician, and Edward Harley (b. 1689, d. 1741), 2nd earl of Oxford and Mortimer, book collector and patron of the arts. Edward Harley bequeathed the library to his widow, Henrietta Cavendish, née Holles (b. 1694, d. 1755) during her lifetime and thereafter to their daughter, Margaret Cavendish Bentinck (b. 1715, d.1785), duchess of Portland; the manuscripts were sold by the Countess and the Duchess in 1753 to the nation for £10,000 (a fraction of their contemporary value) under the Act of Parliament that also established the British Museum; the Harley manuscripts form one of the foundation collections of the British Library.”
Do you not find it odd that, like I said before, all these “ancient manuscripts” somehow make their way through Oxford and/or Cambridge? You claimed in another comment that there are plenty of things that don’t run through there. Please present evidence of that claim in your Member Creation.
What about the Cavendish family being involved? No alarm bells going off in your head? Oh yeah, I forgot, you believe in Space and flying rocks since you’re a “geologist”. Trolol
I have 3 simple questions that I would love to see answered in your MC – 1. how do you know what “Ancient Greek” looks like?; 2. Can you find a single “Ancient manuscript” that doesn’t somehow run through The Vatican, Oxford, or Cambridge?; and 3. Do you have any evidence to support your belief that paper can survive for hundreds of years?
I think that will make for an excellent MC in support of all the history realologist out there.
Finally, do you believe that JLB hid ALL the comments on the entire site, just to hide your jibberish? Ego much?
JLB, I know you’re probably trying to be funny with your comment and the smiley face, but I’m afraid that it may also sound as an admission of guilt, considering how you seem to dislike M.X’s comments, and I frankly don’t understand why.
They seem to me very sensible and to the point, while your replies (and those by watermanchris) appear unnecessarily rude and derogatory. And now you’ve even banned M.X. from commenting again on this article, while offering him a space to publish his observations and research somewhere else as a sweetener.
Since M.X,’s previous comments have been deleted, I cannot list those that I found more pertinent, as you asked me (in a comment that’s been deleted as well, by the way), so I’ll just sum up what I think about your research on the “history hoax” thing, which resonated with M.X.’s observations about it.
Your research on Herodotus’ Histories has cast serious doubts on the veracity of the historical character called “Herodotus” and his alleged work “Histories”, and consequently of History as a discipline in general. But even if you had demonstrated conclusively that Herodotus never existed and that his magnum opus is a work of fiction (although M.X.’s research seems to disagree with the “conclusively” part, and personally I don’t know because I haven’t digged into this myself, but his observations once again seem pertinent to me), from this, as from other demonstrable instances of historical fakery, which are actually abundant at least in recent history) you can suspect that the whole of history has been fabricated, and you may even be right, but I don’t see how it can be said that you have factually demonstrated that all of history is a hoax.
Quite simply, you haven’t produced enough evidence to support your claim. And this not for any particular fault on your part, in my opinion (except maybe a touch of hubris), but simply because it is an impossible task, especially for a single researcher, no matter how brilliant or dedicated. Maybe a team of dedicated researchers could do it in a few years, like for example Simon Shack and other researchers on Cluesforum have conclusively demonstrated 9 11 fakery, or at least try, but it would still be quite a daunting task.
Also because, as I remember M.X. observing in one or more of his disappeared comments, you must demonstrate that artistic masterpieces in history (including many you don’t even know, because no single person can know them all) have been faked in just a couple hundred years or so and how. And to that I add historical monuments, when they’ve actually been built and how.
It’s difficult even to make a list of historical things that may have been faked, imagine to demonstrate conclusively that they have been faked. Impossible, I think.
Therefore, while I appreciate your research and intuition on historical facts (including wars), I think blanket statements like “History is a hoax” or “all wars are hoaxes” are unsubstantiated, and ultimately impossible to substantiate conclusively.
If you want to debate this point with someone who questions it, go ahead and good luck, but I don’t think you can do it convincingly by verbally attacking and denigrating them, like you did with M.X.
I’m not saying this things to piss you off, because that doesn’t interest me in the least nor give me any kind of pleasure. I’m not even interested in debating you further on this, and in fact I didn’t even want to comment, but when I saw someone voicing in a very civil way reasonable doubts similar to mine on your claims, I though it was only right to speak out in his favor, also because everybody else was attacking him, often in much less civil ways.
I hope this comment won’t disappear as well, but even if it does, it’s enough for me if you read it, JLB, although I think M.X.’s observations deserve some support here.
I promise not to comment further on this, anyway, also because I don’t wish to participate in what, far from being a dispute based on facts and evidence, seems to have become just a battle of opinions, which doesn’t interest me anymore, once I’ve expressed mine.
After that, we can agree to disagree, as you like to say, and call it quits. So you won’t even need to ban me too 😉
Jumpy, I think you are in the same boat as mx re history. I would ask you, who is making the first claim? Is it the conventional history? Was that claim substantiated well, do you think? Should it be accepted as a default because it was already in place when you were taught it?
If that original claim is unsubstantiated, and JLB or whoever along and shows that, why does he have to do anything else? He is showing the evidence does not support the claim. The hypothesis we had is out the window. Should we tweak the original? Perhaps, but this should be driven by the evidence. JLB doesn’t need to provide a better story.
PS I think JLB has said there is a technical issue with comments disappearing.
I don’t see how it can be said that you have factually demonstrated that all of history is a hoax.
I haven’t demonstrated that all of history is a hoax, and I haven’t claimed to have demonstrated that all of history is a hoax.
What I have done is take the time to trace the sources of several key narratives and characters of history and shown that the evidence does not support the story we are given.
The sources appear to go back a couple hundred years, perhaps a few hundred years if we are being generous.
Given that I have gotten the same result from every single attempt at tracing the sources for various narratives and characters of history, I have drawn the inference that all of them — all of the characters, all of the narratives — are equally fabricated.
The easiest way for yourself, Gaia/MX, or anybody else to contradict my inference, would be to take the time to trace the sources of some narrative or character of history, and document it for others to see. I would happily publish such research on this very website, an offer I have made to both yourself and Gaia/MX.
For some reason, neither of you have done that, either because you are too lazy to put in the time and effort to do this kind of work, or because you have tried and failed to verify the sources of whatever narrative or character of history you have looked into.
Which is it? Laziness or failure?
Either way, MX has been invited to submit an MC of whatever he believes his ‘research’ to reveal. What he is no longer welcome to do is play his rhetorical games in the comments section of my research articles.
He was given ample opportunity to play with the big boys, and what did he do? Revert to the Figure Eight nonsense which has been his bread and butter for years now.
Nobody has to agree with me about anything on this site; however, if you want to sit there in the comments section of my work and claim that my research is flawed, you’d be well advised to back up your own claims, especially when given several chances to do so.
I think blanket statements like “History is a hoax” or “all wars are hoaxes” are unsubstantiated, and ultimately impossible to substantiate conclusively.
That’s fine, you are welcome to say that ‘some history is a hoax’, however this would imply that some history is real, and if that is the case, I’d like to see the research which led you to this position, to inspect it for myself.
Have you done that research? Where can I inspect it?
I think M.X.’s observations deserve some support here.
The best way for either of you to ‘support the observations’ will be to produce the research.
Again, you are both welcome to send me a doc or pdf of your research and I will gladly publish it as an MC on this very site.
Are either of you going to take up this invitation?
After that, we can agree to disagree, as you like to say, and call it quits.
Indeed. Let’s agree to disagree. I’m always happy to do so.
Agreeing to disagree does not include polluting the comments section of my work with empty rhetoric to undermine my conclusions, without providing a shred of contradictory research.
I hope this is all clear by now.
I’ve said before that there’s a part of me which did not enjoy what happened to Antonio and Reds Rhetoric et al during my respective altercations with them.
These are guys who are external to my operation, and who set themselves up as my adversaries.
Even with these people, a part of me does not enjoy what happens to them when they foolishly try to undermine my research with empty rhetoric.
How do you think I feel about typing up the comment you have just read?
On my own website, in response to people to who at least ostensibly support my operation, do you think I enjoy this kind of interaction?
This is the last place I want to have to go down this path.
If anybody wants to set themselves up as my adversary, I’d much rather they do it externally i.e. away from this site.
That way I can ignore them completely — or, if I feel so inclined, treat them the way I have treated certain adversaries in the past.
There’s a big difference between collegiate and adversarial discourse. I cannot be any more clear about this.
Thank you, JLB, for your quick reply, and for specifying that yours is just an inference. I think myself that each single part of history could be fabricated, or at least twisted or spinned in different ways, so we would even agree 100% if you used the conditional too. But I don’t think everything has been faked starting from just a few hundreds years ago. Can I prove this conclusively? No, and I wouldn’t even try, so you can call it an unsubstantiated opinion, I don’t mind.
Is it because of laziness on my part? Well, maybe, but I’d rather call it insufficient interest, since history has never attracted me much. I’ve always found it impossible to discover exactly what happened in the distant past, especially when I started seeing how people in power are able to falsify even the present, which remains the focus for me anyway. The present, I mean.
So my observations here are not from me as a “fellow researcher”, but from me as part of your audience. And maybe I’m also giving you hints that may stimulate your research for my and other members’ entertainment (if you wanna call it that, since you define yourself also as an entertainer). I try to do it respectfully because I respect your research, even when I find it unconvincing, and I apologize if sometimes this respect doesn’t show enough.
And talking about hints that I could give you, which of course you can disregard completely if you so choose, I think that your case on the history hoax would be more convincing if you managed to demonstrate that also some monuments or works of art like paintings or musical pieces (by Bach or Mozart, for example), and not just books, have been fabricated. But don’t ask me to do that because, as I said, I don’t have enough interest for doing it.
But, as part of your audience, I would love to see that, although I wouldn’t even demand this extra effort on your part, because I know you already do a lot of valuable research for a single person, if it wasn’t because your inferences sound too “grandiose” sometimes (for lack of a better word).
Too grandiose for a researcher, I mean, but probably not for an entertainer, so I guess it depends on what hat you choose to wear each time. 😉
I enjoy them both, anyway, so I take the opportunity to thank you again for your work. And your patience in answering me this time. I appreciate it.
I’m going to but in again (last time, sorry), to provide two sources of information I found on major historical characters.
This interview expresses some major issues re Mozart.
And here’s a great breakdown of Leonardo da Vinci‘s sfumato painting technique. 40 applications at 25 micrometers each, is what gives LdV his no-brush-stroke ‘style’.
In my opinion, there is no reason to believe any of the history as the evidence and experts presenting it are a bust. There are old artifacts there, but who can say anything about them? Eg Rome’s coliseum, 2000 years old, or 300? A gladiatorial arena, or a water reservoir? Who can say?
No need to be sorry, Al. On the contrary, thank you for providing two interesting sources of information, that I will check out ASAP.
I think my last answer to JLB answers another comment of yours as well.
As I said there, I am open to the possibility, and even substantial probability, that everything in history is a fabrication. What I have problems for is mainly the timeline: just a few hundreds year for producing all the variety expressed by the various artistic forms of the world, and also in fields like architecture, for example, seem far too little to me.
Probably you and many other members here live in the “new world”, where things are generally pretty modern and relatively uniform, but if you ever go to Europe, and Italy especially, I think the sheer variety of styles you can find would make it much more difficult for you to wrap your head around the possibility that everything started 300 years ago or so.
That in particular seems to me something that you cannot prove but just believe, and I choose not to believe in anything I cannot prove for whatever reason, including lack of means and/or sufficient interest.
🙂
I’m familiar with the older world too, not Italy but Greece. And London, which has some old bits as well as museums. In Greece I have noticed that there is metal at the center of some of the ancient columns, at least occasionally. The metal looked original, old. This said to me that it was possible that the column pieces were not carved but cast. Where do I put that personal experience?
So, I have problems with the timeline too. I have dismissed the standard narrative, but I can’t even imagine how I could establish a better one. The evidence doesn’t to be there, and I’m not minded to accept the standard narrative.
I’m open to the idea of resets, where in previous times perhaps there have been cataclysmic events. I have seen half buried houses for myself. I can’t think why any architect would design houses in that way! Additionally, there are lots of interesting ‘now and then’ photos to support the idea that earth was deposited around existing houses (they were buried but have now been excavated). I don’t even know that deserts are that old, etc.
So while I would probably put my money on the idea that history stretches back continuously, I don’t think there’s much chance we will ever know it. I’m open to JLBs idea/hypothesis that it was all just created recently, or that the board is swept of people occasionally but that the scenery remains, or even that time is not the set thing we think and may speed up and slow down imperceptibly. (Seems fast at present!) I’ve no reason to think these ideas are true either though, they are (possibly outlandish) possibilities that I have yet to eliminate. I bear them in mind though, as I also consider the experience of the turkey. In its ignorance the turkey believes it is well cared and provided for, only to have to undergo a sudden reappraisal of belief at Christmas!
We just don’t know what we don’t know. Best to base it on the evidence, where there is some, and to dismiss proven liars and their lies. IMO.
I think what this ‘fake history’ angle ultimately comes down to is: can time (and its tie-is-me timed-up and tied-up tameness) be stretched out through mass perception and conception, through symbolic revolutions and re-imaginings? Can 3000 years be squeezed into 300? But what kinds of 3000 years and what kinds of 300 years? Can they even be of the same quality?
Is it possible, given our current experienced rate of growth as human beings to become this ‘beautifully organic’ within the bounds and limitations imposed by that same concept of time? What is a human being according to us and were there other concepts of human beings that we have not been able to access due to our programming? Such as human beings living to 200 years instead of an average of 75 years of pharmaceutically imposed routine of animal training and farming, a system of energy vampirism that passes for a a ‘real and natural’ life? But again, what kind of 200 years and what kind of 75?
Maybe living 200 years of a mechanized and robotic life isn’t even worth 5 years of living in Italy at its best period according to those who have lived there long enough to be able to judge changes in standards of living or the pleasure you can get from day to day living? The quality of life, regardless of the declared economic standards. Certain places may have a low standard of living but a high quality of spiritual interaction of extended-family-comradship with their fellow human beings. That has to be factored in because that makes life more worth living and therefore through more ferment comes more culture and through more culture, more technologies that truly benefit us rather than register on an economic chart, etc.
To what extent are we authentic and to what extent are we programmed beings ruled by our symbolic landscape which was mostly given to us and our ancestors for as long as we have been personally able to experience?
None of us knows personal experience beyond that of meeting maybe our grandparents or great-grandparents, but we did not experience their level of immersion in the present, anymore than the current generation’s feeling for how quick time is passing by would be experienced by us 50-plus year olds in the 1980s and 1970s. Also, when you are a kid of 10, three years seemed like such a long time. High School alone, those three years, seemed to go on forever, just the 3 months of every summer seemed to make you so-much older and so-much a different person than the year before, whereas nowadays, between 2017 and today? It seems that no time has passed at all and very few things have been learned. Things just get more and more polished or not that were maybe learned many years ago.
Drastic hormonal changes in our bodies do not occur like they did in our teenage years (they can, to a certain extent, with high intensity intervals training and the release of HGH, but that’s another topic). What are the teenage years of a society and what are the mature years and what are the decaying years? Are we now in the decaying years? How long before we get back to the infancy and childhood years again? Isn’t that the true reset? And how can there be any true ‘reset’ at all outside of entirely new constructs of language and communication?
So, no, elite-imposed ‘resets’ are to make sure that people are forced back into their psychologically enforced extortion rackets and nothing more. There is no indirect ‘enlightenment’ goal of the secretly ‘benevolent’ elites playing ‘jokes’ on those who deserve to be bamboozled, as some on this very website had Stockholm-Syndromed themselves into believing before the anagram for carnivorous PsyOp put a lock on all our asses at once. The indirect enlightenment after all the dust settles and the psychic vampires have no more blood left to drain, that can only come from the force described as ‘mother nature’ or ‘god,’ the great leveler of the unnatural, the restorer of equilibrium points within and without.
That force which is not farce but includes all man-made farces obviously needs all life to go on in a certain way for a certain purpose we have not yet quite figured out and maybe never will. That force is ultimately benevolent because the possibility of genuine pleasure (play-sure, living in a world where you can play and play-sure, where you know what to do and can do it well and take pleasure form that sureness) or what creates benevolence is something that exists and can be experienced. Fear and what creates malevolence can also be experienced. Both are necessary to balance each other out but healthy survival is a situation where areas where people can play-sure with their pleasures have been identified and the routines of navigating within these areas codified and made habit in that society. The pleasure of playing artificial man-made games within strict rules are analogs of real games of pleasure or displeasure, health or disease, have already been played for a long time in conquering nature more directly.
Games make an art-form of natural challenges, so aspects of them can be experienced with pleasure in safe zones. These games are then bastardized so that those playing them move farther and farther away from the real and end up self-destructing or learning the wrong moves which will not work on ‘god’s or nature’s terms.’ Then to counter this degeneration, other groups spring up that are ‘back to nature,’ and on and on. All you need to do is screw with the foundations a bit, with some fakery, and entire structures are perverted and set on their way for crumbling down civilizations. It’s similar to con-job of the empty Pavlovian plates that were once full and now get masses of doggies salivating at every ring of the same but now w-rung bell. The rite or ritual that ensure the t-root has been gradually removed. Mission accomplished.
https://files.catbox.moe/ruvibm.jpg
https://files.catbox.moe/cadn5s.jpg
https://files.catbox.moe/beqab2.jpg
https://files.catbox.moe/xp3bgz.jpg
Hi Jumpy,
I think you may be missing the point. JLB (as well as myself, TNG, daibpdaibp, al, and anybody else who has gone looking) has done hours and hours (hundreds of hours?) of research into various stories of “history” and has hit the “wire frame mesh” every time. Based on that research, he has drawn the inference that all of what we are told about history is untrue and history only goes back 200-300 years. He never said the authorities don’t have stories. He’s saying that when he tried to double- check their claims, he could only get back a couple hundred years.
What Gaia/MX has done is perform a Google search, found a story, and repeated it here in the comments section of this piece. He basically said – this “looks old” and the experts are saying it’s old, so JLB is wrong.
When challenged on the fact that organic materials cannot last 500+ years, he resorted to ad hominem saying that I “know nothing”. He didn’t cite evidence. When asked about the oldest book he had ever personally held in his hand, he just said “I’ve held a bunch of them but I’m not going to tell you which ones”. This is the exact same thing he did when JLB challenged him back in 2017 on his alleged “family history” that supposedly went back 700 years or something. He has a pattern of this so hopefully you can forgive JLB’s (and my) frustration with his antics.
JLB asked him what he has done to verify the claims of the documents he linked to. His response never came.
He also challenged JLB’s research in another article on the fraud that is “peer review”. JLB said many (most?) academic journals are basically pay to publish. He disagreed with the research and cited 2 journals (out of the thousands of journals currently in publication) that allegedly aren’t pay to publish. So, Gaia clearly shows a pattern of arguing minutia without actually supporting his position that the research is wrong. He is well indoctrinated into the cult of scientism as a “Geologist”. He believes in dinosaurs, spinning ball earth, flying rocks, history, evolution, Peer Review and many of the other tenets of scientism.
We have seen this too many times before to bother wasting time with it, especially in the comments section of a well- researched piece.
Please check out this piece from November of 2017 to understand how long JLB has been putting up with this nonsense from “M.X.” https://www.johnlebon.com/?s=Gaia
I will also caution anybody thinking that Gaia is an ally, whether it be in the war against Fakeology by the realologists, or in any other context. He has had a falling out with every person I have witnessed him “befriend” – Faye/Misom, Geris, Rollo, Mark Tokarski to name 4.
As JLB has offered to publish any of Gaia’s history realology as an MC, I’m not sure what the complaint is.
Setting Gaia aside, I haven’t been able to gather what your thoughts on history are based on your comments. From what I’ve seen, they don’t seem to be very well fleshed out, and please don’t take that as a criticism. I’m genuinely trying to help you work it out. You obviously know that just about everything we were taught in school is wrong. The history that will be written about this Coronavirus hoax, will look nothing like what we are actually living through. They are fabricating numbers and stories in real time, even though people are making videos showing the empty hospitals and nurses are twerking on Tik Tok despite the media claiming they are overrun and the bodies are piling up. Do you really find it such a stretch to imagine that the stories they tell us about the long ago are also fabricated? Do you think it’s possible to know what people were doing or saying thousands of years ago? If you can see that they are obviously lying about the words that were written or spoken, why can’t the entire story be fabricated?
It seems that most of us that know that the TV lies WANT to believe that there was a time, when people were more free, and the people who run the show weren’t in charge. JLB’s history hoax work causes one to realize that that probably wasn’t the case, especially since all the magic documents that can last hundreds or thousands of years go through Oxford, Cambridge and or The Vatican.
Basically, what I’m asking is – Where do you believe hoaxery ends and his story begins? Is there a date for that in your mind? What do you think about this record from the National Archives in the US documenting the 1876 “restoration” of the Declaration of Independence that was supposedly only drafted 100 years prior? Take the time to actually click the link as it will tell you that many of the signatures were unreadable after only 100 years! Are we to believe that American documents from the late 1700s were made of inferior materials to those used thousands of years prior by the “Ancient Greeks”? That only makes sense if you believe the ridiculous story of “the dark ages” where technology went backwards. All organic materials, bones, flesh, plant matter, pigments etc will return to their natural state (dust) if left alone. How did these “manuscripts” avoid this fate? Why don’t any “normal” people find 2,000 year old paper?
I’m sorry of it feels like I’m interrogating you. That is not my intention. I’m am genuinely curious where you stand and why. Maybe I am missing something.
Ciao Watermanchris, and thank you for your interesting and kind comment, in which you make very good points. And don’t worry, I don’t feel interrogated at all, your questions are all legitimate, although I’m not sure I can answer them.
As for where I stand and why, I think I’ve answered this question in my previous answers to JLB’s and Al’s comments.
I hope you won’t consider rude my invitation to read them. Otherwise, please tell me and I’ll copy and paste the most relevant parts for you, no problem.